Question

If the equation to the circle, having double contact with the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ (having eccentricity e) at the needs of a latus rectum, is ${x^2} + {y^2} - ma{e^3}x = {a^2}\left( {1 - {e^2} - {e^4}} \right)$. Find m.

Answer 1

Hint: We will first calculate $x_1$ and $x_2$ from the equation of normal to ellipse to calculate the x – coordinate and then we will calculate the distance in which the radius of the circle will lie. After that, we will calculate the length of the radius of the circle using the distance formula then form the equation of the circle using the x – coordinate and the radius of the circle. We will compare both the equations of the circle (obtained and the given) for the value of m.

Complete step-by-step answer:
 Double contact refers to a point where both the curves, circle and ellipse, will have the same slope and hence same tangent and normal lines.

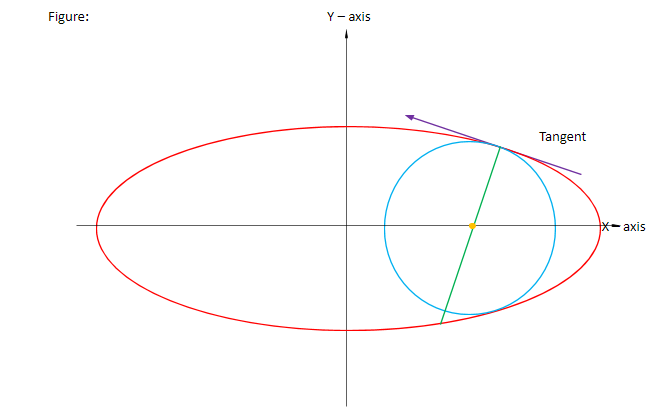
Normal to the circle will also be the normal to the curve therefore, equation of the normal to the ellipse will be:
$ \Rightarrow \dfrac{{{a^2}x}}{{{x_1}}} - \dfrac{{{b^2}y}}{{{y_1}}} = {a^2} - {b^2}$
At $x_1$ = ae and $y_1$ = $\dfrac{{{b^2}}}{a}$ ($x_1$ and $y_1$ are the endpoints of the latus rectum)
This equation of normal to the ellipse will also be the normal to the circle.
And by symmetry, we can say that the centre of the circle will lie at the x – axis.
Putting the value of $x_1$ and $y_1$ in the equation of the normal, we get
$
   \Rightarrow \dfrac{{{a^2}x}}{{ae}} - \dfrac{{{b^2}y}}{{\dfrac{{{b^2}}}{a}}} = {a^2} - {b^2} \\
   \Rightarrow \dfrac{{ax}}{e} - y = {a^2} - {b^2} \\
 $
The x – coordinate will be $ae^3$. Therefore, the radius of the circle will lie between $\left( {ae,\dfrac{{{b^2}}}{a}} \right)$ and ($ae^3$, 0).
Now, we know that $1 - {e^2} = \dfrac{{{b^2}}}{{{a^2}}}$
$ \Rightarrow {b^2} = {a^2}\left( {1 - {e^2}} \right)$$ \Rightarrow {b^4} = {a^4}{\left( {1 - {e^2}} \right)^2}$
 Now, using the distance formula for calculating the radius of the circle, we get
$ \Rightarrow r = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
$
   \Rightarrow r = \sqrt {{{\left( {a{e^3} - ae} \right)}^2} + {{\left( {0 - \dfrac{{{b^2}}}{a}} \right)}^2}} \\
   \Rightarrow r = \sqrt {\left( {{a^2}{e^6} + {a^2}{e^2} - 2{a^2}{e^4}} \right) + \left( {\dfrac{{{b^4}}}{{{a^2}}}} \right)} \\
 $
Putting the value of b4 in the above equation, we get
 \[
   \Rightarrow r = \sqrt {\left( {{a^2}{e^6} + {a^2}{e^2} - 2{a^2}{e^4}} \right) + \left( {\dfrac{{{a^4}{{\left( {1 - {e^2}} \right)}^2}}}{{{a^2}}}} \right)} \\
   \Rightarrow r = \sqrt {\left( {{a^2}{e^6} + {a^2}{e^2} - 2{a^2}{e^4}} \right) + \left( {{a^2}\left( {1 + {e^4} - 2{e^2}} \right)} \right)} \\
   \Rightarrow r = \sqrt {\left( {{a^2}{e^6} + {a^2}{e^2} - 2{a^2}{e^4}} \right) + \left( {{a^2} + {a^2}{e^4} - 2{a^2}{e^2}} \right)} \\
   \Rightarrow r = \sqrt {{a^2}{e^6} + {a^2} - {a^2}{e^4} - {a^2}{e^2}} \\
 \]
Squaring both sides, we get
$ \Rightarrow {r^2} = {a^2}{e^6} + {a^2} - {a^2}{e^4} - {a^2}{e^2}$
Now, we know that the equation of the circle is (x – x1)2 + (y – y1)2 = r2
Substituting the values of x1, y1 and r, we get
$
   \Rightarrow {\left( {x - a{e^3}} \right)^2} + {\left( {y - 0} \right)^2} = {a^2}{e^6} + {a^2} - {a^2}{e^4} - {a^2}{e^2} \\
   \Rightarrow {x^2} + {a^2}{e^6} - 2a{e^3}x + {y^2} = {a^2}{e^6} + {a^2} - {a^2}{e^4} - {a^2}{e^2} \\
   \Rightarrow {x^2} + {y^2} - 2a{e^3}x = {a^2} - {a^2}{e^2} - {a^2}{e^4} \\
   \Rightarrow {x^2} + {y^2} - 2a{e^3}x = {a^2}\left( {1 - {e^2} + {e^4}} \right) \\
 $
Comparing it with the given equation of the circle: ${x^2} + {y^2} - ma{e^3}x = {a^2}\left( {1 - {e^2} - {e^4}} \right)$
We get the value of m = 2.

Note: In such questions, you may get confused at a lot of places like while reducing the x – coordinate and while calculating the radius from the distance formula using the coordinates. Be careful in simplification of the equation of radius.