Question

If the distance between a 13-foot ladder and a vertical wall is 5 feet along the ground, how high can a person climb if the ladder is inclined against the wall?
(a) 18 feet
(b) 65 feet
(c) $\dfrac{13}{5}$ feet
(d) 8 feet
(e) 12 feet

Answer 1

Hint: We start solving the problem by drawing the given information. After drawing, we can see that the given information holds everything in a right-angled triangle. We use the Pythagoras theorem to find the required side of the triangle, which is the height that a person climbs if the ladder is inclined against the wall.

Complete step by step answer:
Given that the distance between a 13-foot ladder and a vertical wall is 5 feet along the ground. The ladder is placed inclined against the wall. We need to find the vertical distance of the wall that a person can climb.
Let us draw the given situation to get the better view.
 

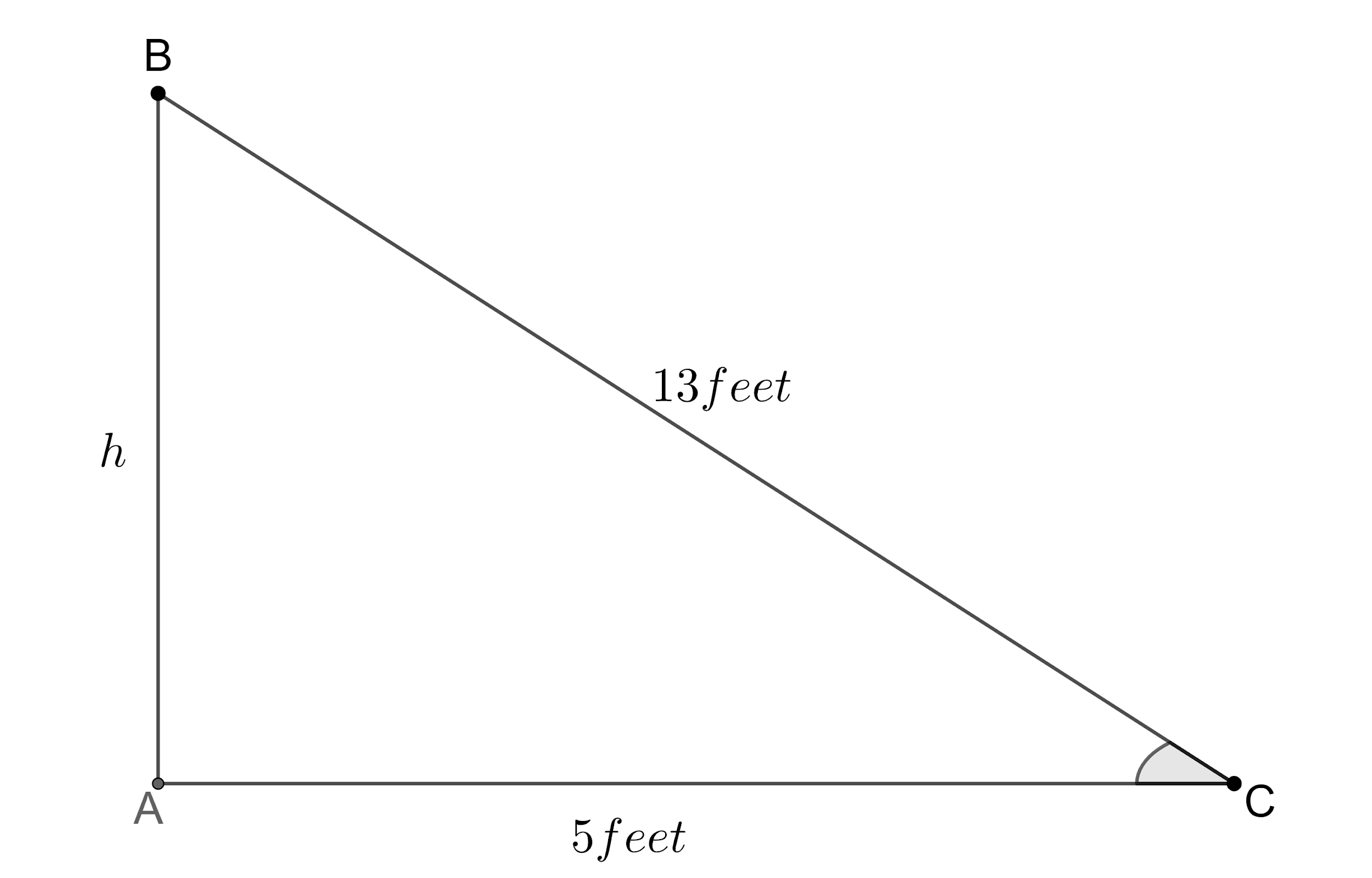
Let us assume AB be the vertical wall and height of the vertical be ‘h’ feet. Here BC is the length of the ladder and AC be the horizontal distance between base of vertical wall AB and base of the ladder.
We can see that the given triangle ABC is a right-angled triangle. We make use of the Pythagoras theorem to find the length of the side AB.
We know that according to the Pythagoras theorem, the sum of squares of the other two sides of the right-angled triangle is equal to the square of the hypotenuse of that triangle.
$\Rightarrow $ $A{{B}^{2}}+C{{A}^{2}}=B{{C}^{2}}$.
$\Rightarrow $ ${{h}^{2}}+{{5}^{2}}={{13}^{2}}$.
$\Rightarrow $ ${{h}^{2}}+25=169$.
$\Rightarrow $ ${{h}^{2}}=169-25$.
$\Rightarrow $ ${{h}^{2}}=144$.
$\Rightarrow $ $h=\sqrt{144}$.
$\Rightarrow $ h = 12.
We have found the height that a person can climb the wall using a ladder is 12 feet.

So, the correct answer is “Option E”.

Note: We should not take the negative root value (–12) for h, as the height cannot be negative. We can alternatively do the problem as follows:
From the triangle ABC, $\cos C=\dfrac{5}{13}$.
We know that $\sin C=\sqrt{1-{{\cos }^{2}}C}$.
$\Rightarrow $ $\sin C=\sqrt{1-{{\left( \dfrac{5}{13} \right)}^{2}}}$.
$\Rightarrow $ $\sin C=\sqrt{1-\left( \dfrac{25}{169} \right)}$.
$\Rightarrow $ $\sin C=\sqrt{\left( \dfrac{169-25}{169} \right)}$.
$\Rightarrow $ $\sin C=\sqrt{\dfrac{144}{169}}$.
$\Rightarrow $ $\sin C=\dfrac{12}{13}$.
$\Rightarrow $ $\dfrac{AB}{BC}=\dfrac{12}{13}$.
$\Rightarrow $ $\dfrac{AB}{13}=\dfrac{12}{13}$.
$\Rightarrow $ AB = 12.
We have found the value of AB as 12 feet.