Question

If the coefficient of friction between the surface of 25 kg block and fixed vertical wall is 0.4, and that between both the blocks is also 0.4. All the shown pulleys are light and frictionless; strings are light, perfectly inextensible and smooth. Then (Take $g = 10\;m/{s^2}$)

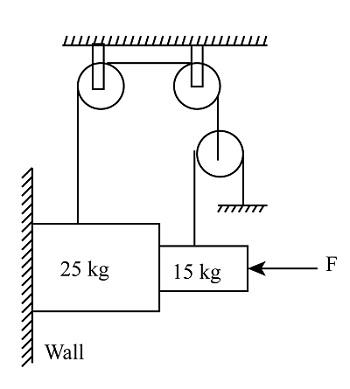
(A) to have the complete system in static equilibrium, the magnitude of minimum horizontal force F towards right (as shown) is equal to $\dfrac{{125}}{4}\;N$.
(B) to have the complete system in static equilibrium, the magnitude of minimum horizontal force F towards right (as shown) is equal to 125 N.
(C) in the equilibrium state, the direction of frictional force exerted by vertical wall on 25 kg block and the direction of friction exerted by 25 kg block on 15 kg block, downwards & upwards, respectively.

(D) in the equilibrium state, the direction of frictional force exerted by vertical wall on 25 kg block and the direction of frictional force exerted by 25 kg block on 15 kg block ,upwards or downwards, respectively.

Answer 1

Hint: In the question, lots of information about the assembly is given; with the help of these information, make the free body diagram of the pulley and blocks. After this, resolve all forces and build the relation between various forces to determine the applied force's magnitude

 Complete step by step answer:
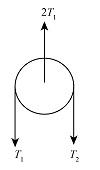
The free-body diagram of the pulley which above the 25 kg block is,

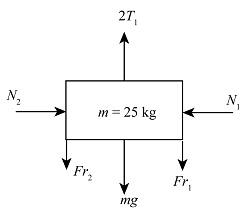
The free-body diagram of the25 kg block is,

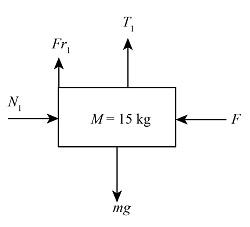
The free-body diagram of the 15 kg block is,

First, we will resolve the forces that are acting on the 25 kg block.

Therefore we get,

$2{T_1} = {f_{r2}} + mg + {f_{r1}}$...... (1)

Here, ${T_1}$ is the tension force and ${f_{r1}}$ is the frictional force acting due to the other block ${f_{r2}}$ is the frictional force due to the wall, $g$ is the acceleration due to gravity, and $m$ is the mass of the large block.

Now resolve the forces that are acting on the 15 kg pulley.

${T_1} + {f_{r1}} = Mg$...... (2)

Here $M$ is the mass of the small block.

Here applied force is acting as normal force, and we know that the product of the normal force and coefficient of friction gives the magnitude of the frictional force; therefore, we get

${f_{r1}} = {f_{r2}} = \mu F$...... (3)

Here, $F$ is the applied force, and $\mu $ is the coefficient of friction.

Substitute the value of the coefficient of friction in the above equation.

${f_{r1}} = {f_{r2}} = 0.4F$...... (4)

Multiply equation (2) by 2, so that magnitude of the tension force becomes equal in equation (1) and (2), so

$\begin{array}{l}
2{T_1} + 2{f_{r1}} = 2Mg\\
2{T_1} = 2Mg - 2{f_{r1}}
\end{array}$...... (5)

Now, use the equation (1) and (5) to determine the applied force F.

\[\begin{array}{l}
{f_{r2}} + mg + {f_{r1}} = 2Mg - 2{f_{r1}}\\
{f_{r2}} = 2Mg - mg - 3{f_{r1}}
\end{array}\]

Substitute the values in the above equation.

Therefore, we get

$\begin{array}{l}
0.4F = 2\left( {15\;{\rm{kg}} \times {\rm{10}}\;{\rm{m/}}{{\rm{s}}^2}} \right) - \left( {25\;{\rm{kg}} \times {\rm{10}}\;{\rm{m/}}{{\rm{s}}^2}} \right) - 3\left( {0.4F} \right)\\
0.4F = 300\;{\rm{N}} - 250\;{\rm{N}} - 1.2F\\
F = \dfrac{{50\;{\rm{N}}}}{{1.6}}\\
F = \dfrac{{50\;{\rm{N}}}}{{4\left( {0.4} \right)}}
\end{array}$

On further solving the above equation, we get

$F = \dfrac{{125}}{4}\;{\rm{N}}$

The friction force between the wall and block will be opposite to the frictional force between two blocks.
Therefore, if the coefficient of friction between the surface of a 25 kg block and the fixed vertical wall is 0.4, and that between both the blocks is also 0.4. All the shown pulleys are light and frictionless; strings are light, perfectly inextensible, and smooth. Then to have the complete system in static equilibrium, the magnitude of minimum horizontal force F towards the right will be equal to $\dfrac{{125}}{4}\;N$and in the equilibrium state, the direction of frictional force exerted by the vertical wall on 25 kg block and the direction of frictional exerted by 25 kg block on 15 kg block, downwards & upwards, respectively.

So, the correct OPTIONS are “Option A and C”.

Note:
In these types of questions, always make the separate free-body diagrams of all the objects because it gives clear information about the forces. If we make only one free body diagram of the assembly, confusion can arise, and due to this, we use the wrong sign convention or wrong values in the calculation.