Question

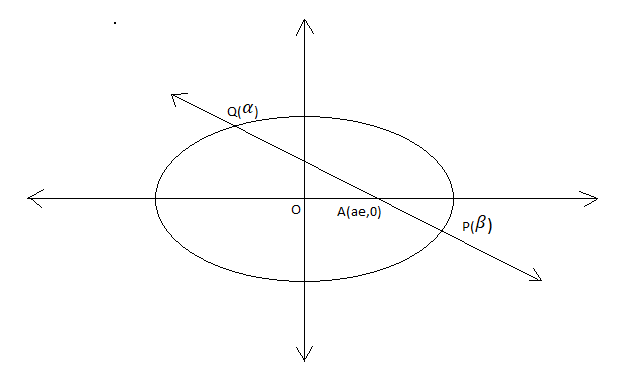
If the chord through the points whose eccentric angles are \[\alpha \] and \[\beta \] on the ellipse \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] passes through the focus (ae, 0), then the value of \[\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2}\] is:
A. \[\dfrac{e+1}{e-1}\]
B. \[\dfrac{e-1}{e+1}\]
C. \[\dfrac{e+1}{e-2}\]
D. none

Answer 1

Hint: We will first write the equation of the chord to the ellipse with given eccentric angles and then we will put the point (ae, 0) in the equation as it is passing through it so it will satisfy the equation.

Complete step-by-step answer:
We have been given the eccentric angle of chord as \[\alpha \] and \[\beta \] on the ellipse \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\].
The eccentric angle of a point on an ellipse with semi major axes of length and semi minor axes of length is the angle in the parametrization.
Now the equation of chord to the ellipse with eccentric angle \[\alpha \] and \[\beta \] is as follows:
\[\dfrac{x}{a}\cos \dfrac{\alpha +\beta }{2}+\dfrac{y}{b}\sin \dfrac{\alpha +\beta }{2}=\cos \dfrac{\alpha -\beta }{2}\]
It is given that it passes through (ae, 0).
\[\begin{align}
  & \dfrac{ae}{a}\cos \dfrac{\alpha +\beta }{2}+\dfrac{0}{b}\sin \dfrac{\alpha +\beta }{2}=\cos \dfrac{\alpha -\beta }{2} \\
 & e\cos \left( \dfrac{\alpha }{2}+\dfrac{\beta }{2} \right)=\cos \left( \dfrac{\alpha }{2}-\dfrac{\beta }{2} \right) \\
\end{align}\]
Now we are using the trigonometric identity which is given as below.
\[\begin{align}
  & \cos \left( A+B \right)=\cos A\cos B-\sin A\sin B \\
 & C=\cos \left( A-B \right)=\cos A\cos B+\sin A\sin B \\
 & \Rightarrow e\left( \cos \dfrac{\alpha }{2}\cos \dfrac{\beta }{2}-\sin \dfrac{\alpha }{2}\sin \dfrac{\beta }{2} \right)=\cos \dfrac{\alpha }{2}\cos \dfrac{\beta }{2}+\sin \dfrac{\alpha }{2}\sin \dfrac{\beta }{2} \\
\end{align}\]
Now taking the term \[\left( \cos \dfrac{\alpha }{2}\cos \dfrac{\beta }{2} \right)\] as common from both sides of the equality, we get as follows:
\[\begin{align}
  & e\cos \dfrac{\alpha }{2}\cos \dfrac{\beta }{2}\left( 1-\dfrac{\sin \dfrac{\alpha }{2}\sin \dfrac{\beta }{2}}{\cos \dfrac{\alpha }{2}\cos \dfrac{\beta }{2}} \right)=\cos \dfrac{\alpha }{2}\cos \dfrac{\beta }{2}\left( 1+\dfrac{sin\dfrac{\alpha }{2}\sin \dfrac{\beta }{2}}{\cos \dfrac{\alpha }{2}\cos \dfrac{\beta }{2}} \right) \\
 & e\left( 1-\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2} \right)=1+\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2} \\
 & e-e\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2}=1+\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2} \\
 & e-1=(1+e)\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2} \\
 & \dfrac{e-1}{1+e}=\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2} \\
\end{align}\]
Therefore, we have proved that \[\dfrac{e-1}{1+e}\] = \[\tan \dfrac{\alpha }{2}\tan \dfrac{\beta }{2}\].
Hence the correct answer of the above mentioned question is option B.

Note: Be careful while substituting the values of \[\left( \cos \dfrac{\alpha }{2}+\cos \dfrac{\beta }{2} \right)\] and \[\left( \cos \dfrac{\alpha }{2}-\cos \dfrac{\beta }{2} \right)\] as there is a chance that you might put the wrong sign.
Also, be careful while choosing the option sometime when you choose option A in spite of option B.