Question

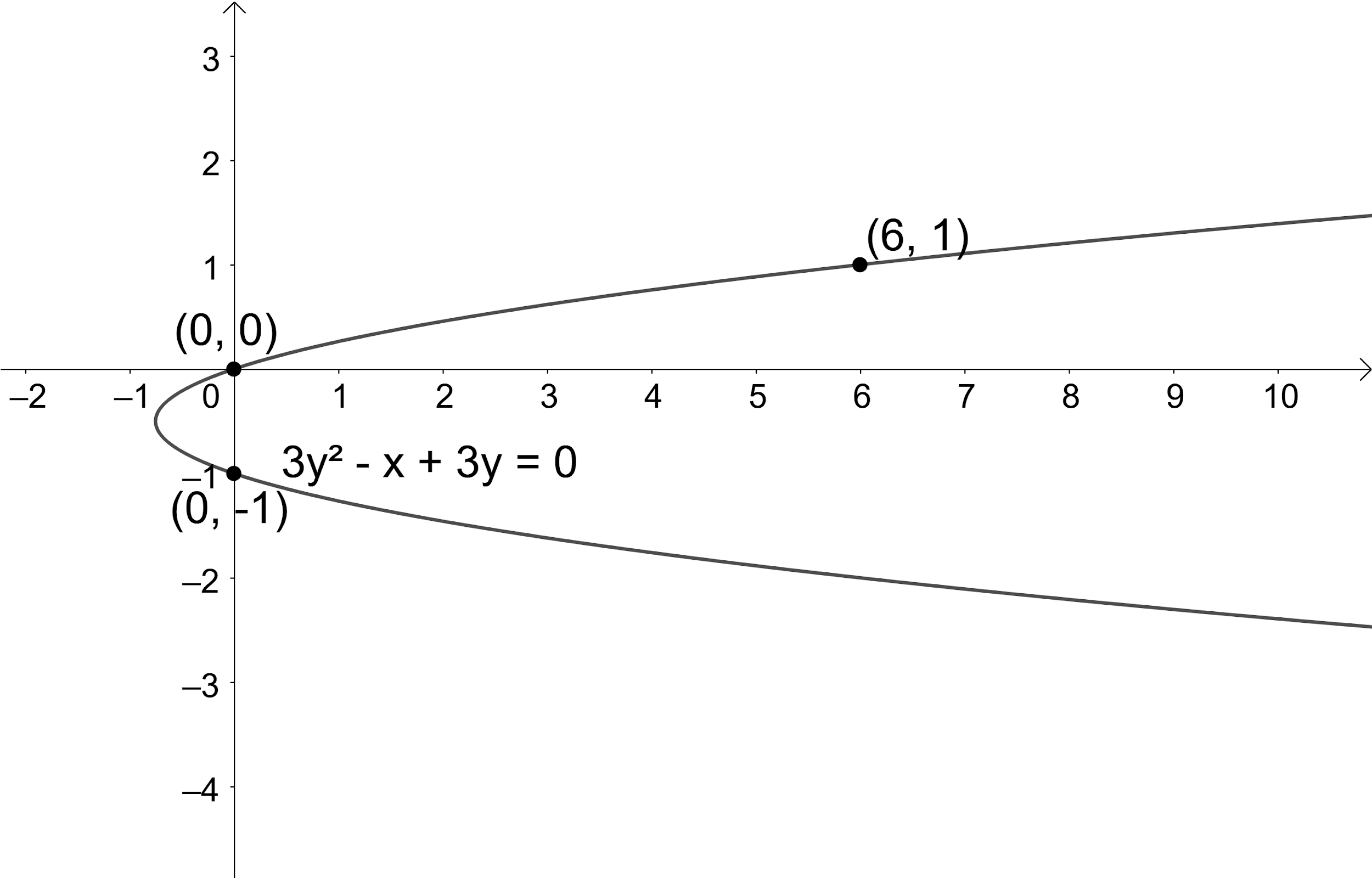
If the axis of the parabola is horizontal and it passes through the points $\left( 0,0 \right)$, $\left( 0,-1 \right)$ and $\left( 6,1 \right)$, then find its equation?
(a) ${{y}^{2}}+3y-x-4=0$
(b) ${{y}^{2}}+3y+x-4=0$
(c) ${{y}^{2}}-3y-x-4=0$.
(d) None of these

Answer 1

Hint: We start solving the problem by recalling the general equation of the parabola whose axis is horizontal as ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$. We then substitute the points $\left( 0,0 \right)$, $\left( 0,-1 \right)$ and $\left( 6,1 \right)$ each at once to get the relations between ‘h’, ‘k’ and ‘a’. We then make the necessary calculations between these three relations to get the values of ‘h’, ‘k’ and ‘a’. We then substitute these values in the general equation of parabola to get the required equation.

Complete step by step answer:
According to the problem, we are given that the axis of the parabola is horizontal and we need to find the equation of parabola if it passes through the points $\left( 0,0 \right)$, $\left( 0,-1 \right)$ and $\left( 6,1 \right)$.

We know that the general equation of the parabola is ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$, if the axis of the parabola is horizontal.
Let us substitute the point $\left( 0,0 \right)$ in the parabola ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$.
So, we get ${{\left( 0-k \right)}^{2}}=4a\left( 0-h \right)$.
$\Rightarrow {{k}^{2}}=-4ah$ ---(1).
Let us substitute the point $\left( 0,-1 \right)$ in the parabola ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$.
So, we get ${{\left( -1-k \right)}^{2}}=4a\left( 0-h \right)$.
$\Rightarrow {{k}^{2}}+2k+1=-4ah$.
From equation (1) we get ${{k}^{2}}+2k+1={{k}^{2}}$.
$\Rightarrow 2k+1=0$.
$\Rightarrow 2k=-1$.
$\Rightarrow k=\dfrac{-1}{2}$ ---(2).
Let us substitute equation (2) in equation (1), we get
$\Rightarrow {{\left( \dfrac{-1}{2} \right)}^{2}}=-4ah$.
$\Rightarrow \dfrac{1}{4}=-4ah$.
$\Rightarrow h=\dfrac{-1}{16a}$ ---(3).
Let us substitute the point $\left( 6,1 \right)$ in the parabola ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$.
So, we get ${{\left( 1-k \right)}^{2}}=4a\left( 6-h \right)$.
From equations (2) and (3), we get ${{\left( 1+\dfrac{1}{2} \right)}^{2}}=4a\left( 6-\left( \dfrac{-1}{16a} \right) \right)$.
$\Rightarrow {{\left( \dfrac{3}{2} \right)}^{2}}=4a\left( 6+\dfrac{1}{16a} \right)$.
$\Rightarrow \dfrac{9}{4}=24a+\dfrac{1}{4}$.
$\Rightarrow 2=24a$.
$\Rightarrow a=\dfrac{1}{12}$ ---(4).
Let us substitute equation (4) in equation (3).
So, we get $h=\dfrac{-1}{16\left( \dfrac{1}{12} \right)}=\dfrac{-3}{4}$ ---(5).
Let us substitute the values of ‘h’, ‘k’ and ‘a’ obtained from equations (2), (4) and (5) in ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$.
So, we get ${{\left( y+\dfrac{1}{2} \right)}^{2}}=4\left( \dfrac{1}{12} \right)\left( x+\dfrac{3}{4} \right)$.
$\Rightarrow {{y}^{2}}+y+\dfrac{1}{4}=\left( \dfrac{1}{3} \right)\left( x+\dfrac{3}{4} \right)$.
$\Rightarrow 3{{y}^{2}}+3y+\dfrac{3}{4}=x+\dfrac{3}{4}$.
$\Rightarrow 3{{y}^{2}}+3y-x=0$.
So, we have found the equation of the parabola as $3{{y}^{2}}+3y-x=0$.

So, the correct answer is “Option d”.

Note: We can also take the general equation of the parabola whose axis is horizontal (axis is parallel to x-axis) as $x=a{{y}^{2}}+by+c$ which can be solved as shown below.
Let us substitute the point $\left( 0,0 \right)$ in $x=a{{y}^{2}}+by+c$.
So, we get $0=a{{\left( 0 \right)}^{2}}+b\left( 0 \right)+c$.
$\Rightarrow 0=0+0+c$.
$\Rightarrow c=0$ ---(6).
Let us substitute the point $\left( 0,-1 \right)$ in $x=a{{y}^{2}}+by+c$.
So, we get $0=a{{\left( -1 \right)}^{2}}+b\left( -1 \right)+c$.
From equation (6).
$\Rightarrow 0=a-b+0$.
$\Rightarrow a-b=0$ ---(7).
Let us substitute the point $\left( 6,1 \right)$ in $x=a{{y}^{2}}+by+c$.
So, we get $6=a{{\left( 1 \right)}^{2}}+b\left( 1 \right)+c$.
From equation (6).
$\Rightarrow 6=a+b+0$.
$\Rightarrow a+b=6$ ---(8).
On solving equations (7) and (8), we get $a=3$ and $b=3$.
So, we get the equation of the parabola as $x=3{{y}^{2}}+3y+0$.
$\Rightarrow 3{{y}^{2}}+3y-x=0$.