Question

If one diagonal of a trapezium divides the other diagonal in the ratio of 1:3. Prove that one of the parallel sides is three times the other.

Answer 1

Hint: First of all draw a trapezium and then draw two diagonals in the trapezium. Then take the two triangles which are part of the trapezium in such a way that one of the sides of both the triangles is the parallel sides of the trapezium. Now, prove the similarity of these two triangles and then using the property of similar triangles that the sides of the similar triangles are proportional to each other to show that one of the parallel sides of the trapezium is three times the other.

Complete step-by-step solution -
In the below diagram, we have shown a trapezium ABCD and the two diagonals AC and BD such that both these diagonals intersect at point E.
   

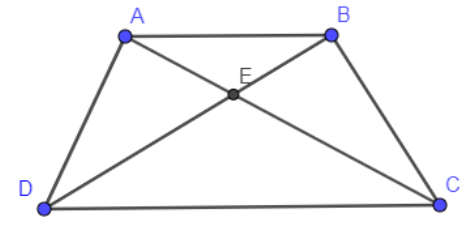
In the above figure, AB and DC are the parallel sides of the trapezium.
It is given that one of the diagonals of the trapezium divides the other in the ratio of 1:3 so applying this definition in the diagram that we have drawn we get,
$\dfrac{DE}{EB}=\dfrac{3}{1}$
We have to prove that DC = 3AB.
To prove that DC = 3AB we are going to first prove the similarity of the triangles DEC and AEB.
In $\Delta DEC\And \Delta AEB$,
AB is parallel to DC and AC, BD are transversals so we $\angle DEC\And \angle AEB$ are vertically opposite angles and vertically opposite angles are equal to each other.
$\angle DEC=\angle AEB$
AB is parallel to DC and BD is transversal so $\angle ABE\And \angle EDC$ are alternate interior angles and we know that alternate interior angles are equal to each other.
$\angle ABE=\angle EDC$
So by AA similarity condition, we can say that $\Delta DEC$ is similar to $\Delta AEB$.
We know that, if two triangles are similar then ratios of their corresponding sides are equal.
$\dfrac{DE}{EB}=\dfrac{DC}{AB}$……………Eq. (1)
And we have shown above that:
$\dfrac{DE}{EB}=\dfrac{3}{1}$
Substituting the above relation in eq. (1) we get,
$\dfrac{3}{1}=\dfrac{DC}{AB}$
On cross-multiplying the above relation, we get,
$3AB=DC$
Hence, we have proved that DC = 3AB.

Note: To do this question, your concepts regarding the properties of trapezium, properties of similar triangles, conditions of similarity of the two triangles must be clear. In general, you will see questions quite often utilizing the property of similar triangles that the ratio of the corresponding sides of the triangles are equal so you should have the sound knowledge of this property.