Question

If in a triangle ABC $\angle C=60{}^\circ $, then prove that $\dfrac{1}{a+c}+\dfrac{1}{b+c}=\dfrac{3}{a+b+c}$

Answer 1

Hint: Apply cosine rule on angle C, i.e. use $\cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$. Use the fact that $\cos 60{}^\circ =\dfrac{1}{2}$. Simplify the resulting expression to get the result.

Complete step-by-step answer:

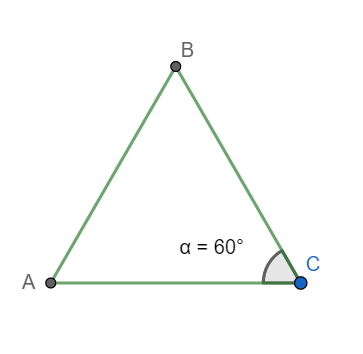
Here as per usual notation, we have a = BC, b = AC and c = AB.
We know that in any triangle ABC, we have $\cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$ (cosine rule)
Applying cosine rule on triangle ABC, we get
$\cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$
We know that $\cos 60{}^\circ =\dfrac{1}{2}$
Since $C=60{}^\circ $, we have $\cos C=\dfrac{1}{2}$
Hence, we have
$\dfrac{1}{2}=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$
Multiplying by 2 on both sides, we get
$\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{ab}=1$
Adding and subtracting 2ab in numerator, we get
$\begin{align}
  & \dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}+2ab-2ab}{ab}=1 \\
 & \Rightarrow \dfrac{{{a}^{2}}+2ab+{{b}^{2}}-{{c}^{2}}-2ab}{ab}=1 \\
\end{align}$
We know that ${{a}^{2}}+2ab+{{b}^{2}}={{\left( a+b \right)}^{2}}$
Using the above identity, we get
$\dfrac{{{\left( a+b \right)}^{2}}-{{c}^{2}}-2ab}{ab}=1$
We know that $\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$
Using the above identity, we get
$\begin{align}
  & \dfrac{{{\left( a+b \right)}^{2}}-{{c}^{2}}}{ab}-\dfrac{2ab}{ab}=1 \\
 & \Rightarrow \dfrac{{{\left( a+b \right)}^{2}}-{{c}^{2}}}{ab}-2=1 \\
 & \Rightarrow \dfrac{{{\left( a+b \right)}^{2}}-{{c}^{2}}}{ab}=3 \\
\end{align}$
We know that ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$
Using the above identity, we get
$\dfrac{\left( a+b+c \right)\left( a+b-c \right)}{ab}=3$
Dividing both sides by a+b+c, we get
$\dfrac{a+b-c}{ab}=\dfrac{3}{a+b+c}$
Also, we have
$\begin{align}
  & \dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}=2 \\
 & \Rightarrow \\
\end{align}$
Now, we have
$\dfrac{a+b-c}{ab}=\dfrac{3}{a+b+c}$
We know that $\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$
Using the above identity, we have
$\begin{align}
  & \dfrac{a}{ab}+\dfrac{b}{ab}-\dfrac{c}{ab}=\dfrac{3}{a+b+c} \\
 & \Rightarrow \dfrac{1}{b}+\dfrac{1}{a}-\dfrac{c}{ab}=\dfrac{3}{a+b+c} \\
\end{align}$
In the first fraction on LHS, multiply the numerator and denominator by b+c and in the second fraction on LHS, multiply the numerator and denominator by a+c, we get
$\begin{align}
  & \dfrac{b+c}{b\left( b+c \right)}+\dfrac{a+c}{a\left( a+c \right)}-\dfrac{c}{ab}=\dfrac{3}{a+b+c} \\
 & \Rightarrow \dfrac{1}{b+c}\left[ \dfrac{b+c}{b} \right]+\dfrac{1}{a+c}\left[ \dfrac{a+c}{a} \right]-\dfrac{c}{ab}=\dfrac{3}{a+b+c} \\
\end{align}$
Now we know that $\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$
Applying the above identity, we get
$\begin{align}
  & \dfrac{1}{b+c}\left[ 1+\dfrac{c}{b} \right]+\dfrac{1}{a+c}\left[ 1+\dfrac{c}{a} \right]-\dfrac{c}{ab}=\dfrac{3}{a+b+c} \\
 & \Rightarrow \dfrac{1}{b+c}+\dfrac{1}{a+c}+\dfrac{c}{a\left( a+c \right)}+\dfrac{c}{b\left( b+c \right)}-\dfrac{c}{ab}=\dfrac{3}{a+b+c} \\
 & \Rightarrow \dfrac{1}{b+c}+\dfrac{1}{a+c}+\dfrac{c}{ab\left( a+c \right)\left( b+c \right)}\left[ b\left( b+c \right)+a\left( a+c \right)-\left( a+c \right)\left( b+c \right) \right]=\dfrac{3}{a+b+c} \\
\end{align}$
Expanding the terms, we get
$\begin{align}
  & \dfrac{1}{a+c}+\dfrac{1}{b+c}+\dfrac{c}{ab\left( a+c \right)\left( b+c \right)}\left( {{b}^{2}}+bc+{{a}^{2}}+ac-ab-ac-bc-{{c}^{2}} \right)=\dfrac{3}{a+b+c} \\
 & \Rightarrow \dfrac{1}{a+c}+\dfrac{1}{b+c}+\dfrac{c}{ab\left( b+c \right)\left( a+c \right)}\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}}-ab \right)=\dfrac{3}{a+b+c} \\
\end{align}$
We know that
${{a}^{2}}+{{b}^{2}}-{{c}^{2}}-ab=0$ (proved above)
Hence we have
$\begin{align}
  & \dfrac{1}{a+c}+\dfrac{1}{b+c}-0=\dfrac{3}{a+b+c} \\
 & \Rightarrow \dfrac{1}{a+c}+\dfrac{1}{b+c}=\dfrac{3}{a+b+c} \\
\end{align}$


Note: In the questions of the above type, we need to understand which formula to apply and which not. Cosine rule is generally applied when on the basis of a known angle we want to find the relations between the sides of the triangle as is the case above.
[2] Alternatively, we can solve the above question by showing that $\dfrac{1}{a+c}+\dfrac{1}{b+c}=\dfrac{3}{a+b+c}\Leftrightarrow {{a}^{2}}+{{b}^{2}}-{{c}^{2}}=ab$
Multiply both sides of the equation by (a+b)(b+c)(a+b+c) and simplify to prove the above result.