Question

If $ \Delta ABC\cong \Delta DEF $ by SSS congruence rule then
a. AB = EF, BC = FD, CA = DE
b. AB = FD, BC = DE, CA = EF
c. AB = DE, BC = EF, CA = FD
d. AB = DE, BC = EF, $ \angle C=\angle F $

Answer 1

HintTo find the solution of this question, we will take help of the basic definition of SSS congruence rule. SSS means side side side, and SSS congruency means that all the sides of two triangles will be equal.

Complete step-by-step answer:
It is given in the question that $ \Delta ABC\cong \Delta DEF $ by SSS congruence rule and we have been asked to find the most appropriate options for this condition. Here, $ \cong $ means congruent and SSS means side side side. So, basically we have two different triangles, $ \Delta ABC $ is the first triangle and $ \Delta DEF $ is the second triangle.
Here, we can say that $ \Delta ABC $ is congruent to $ \Delta DEF $ by SSS congruence rule. We know that SSS congruence rule states that if two different triangles have exactly the same measurement of all the sides, then it means that they are congruent to each other.
Thus, we can say that all the sides of $ \Delta ABC $ are equal to all the sides of $ \Delta DEF $ .

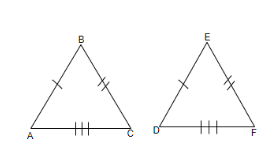
We get AB = DE, BC = EF and AC = DF. Now, we will check which of the options satisfies this condition, where all the sides of the two triangles are equal.
So, we get that option (c) matches our condition, that is AB = DE, BC = EF and AC = DF.
Hence, option (c) is the correct answer.

Note: Students may misunderstand SSS congruency and think that if two different triangles have all the sides equal then they are equilateral triangles, like in this question, they might assume it as, AB = BC = CA = DE = EF = FD, but this is wrong. Students should also note to compare corresponding sides properly, triangles ABC and DEF should be drawn properly so that the vertices are in a cyclic order.