Question

If any tangent to the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ intercepts equal length $'l'$ on the axes, then $l$ is equal to
$\left( A \right)\text{ }{{a}^{2}}+{{b}^{2}}$
$\left( B \right)\text{ }\sqrt{{{a}^{2}}+{{b}^{2}}}$
$\left( C \right)\text{ }{{\left( {{a}^{2}}+{{b}^{2}} \right)}^{2}}$
$\left( D \right)\text{None of these}$

Answer 1

Hint: In this question we have been given with the equation of an ellipse and we have been given that any tangent to the ellipse intercepts equal length $l$ then we have to find the value of $l$. We will solve this question by first writing the equation of the tangent to the given ellipse at a point $P\left( a\cos \theta ,b\sin \theta \right)$ and then we will find the intercept of the line on the axes. We will then use the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$ and solve the expression to get the required solution.

Complete step-by-step solution:
Here we have been provided with the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ on which a tangent is drawn cutting intercepts of equal lengths ‘I’ on the axes. We are asked to determine the value of l. First let us draw a diagram of the given situation.

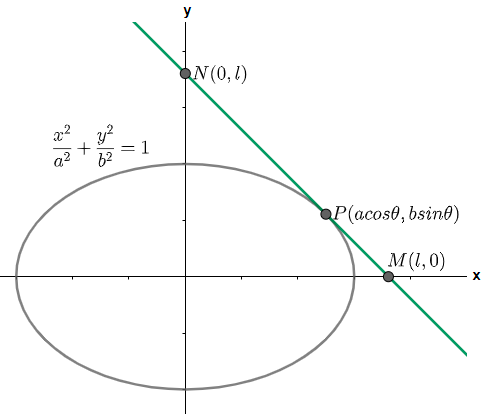
Now, in the above figure we have assumed that the tangent is drawn to the ellipse at point P which lies in the first quadrant and this tangent line intersects the x – axis at point M and y – axis at point N. The point P is assumed as $P\left( a\cos \theta ,b\sin \theta \right)$ which is the general assumption we make while assuming a point on the ellipse.
Since, length of the intercepts are equal and is l, so we have the coordinates of point M as (l, 0) and that of point N as (0, a). So using the formula $\dfrac{\Delta y}{\Delta x}$ for finding the slope of the line MN we have,
$\Rightarrow $ Slope of line MN = $\dfrac{0-l}{l-0}$
$\Rightarrow $ Slope of line MN = -1
Now, the slope of the tangent line MN at point P will be obtained by differentiating the equation of the ellipse and substituting the value of the coordinates in the expression of $\dfrac{dy}{dx}$, therefore on differentiating we get,
$\begin{align}
  & \Rightarrow \dfrac{2x}{{{a}^{2}}}+\dfrac{2y}{{{b}^{2}}}\left( \dfrac{dy}{dx} \right)=0 \\
 & \Rightarrow \left( \dfrac{dy}{dx} \right)=\left( -\dfrac{x}{{{a}^{2}}} \right)\times \left( \dfrac{{{b}^{2}}}{y} \right) \\
\end{align}$
Substituting the value of the coordinates and that of the slope of the tangent line we get,
$\begin{align}
  & \Rightarrow -1=\left( -\dfrac{a\cos \theta }{{{a}^{2}}} \right)\times \left( \dfrac{{{b}^{2}}}{b\sin \theta } \right) \\
 & \Rightarrow -1=\dfrac{-b}{a}\cot \theta \\
 & \Rightarrow \tan \theta =\dfrac{b}{a} \\
\end{align}$
Now, we know that $\tan \theta =\dfrac{P}{B}$ where P = perpendicular and B = base, so using the Pythagoras theorem ${{H}^{2}}={{P}^{2}}+{{B}^{2}}$ where H = hypotenuse we get,
\[\Rightarrow H=\sqrt{{{a}^{2}}+{{b}^{2}}}\]
We know that $\sin \theta =\dfrac{P}{H}$ and $\cos \theta =\dfrac{B}{H}$ so substituting the values we get,
$\Rightarrow \sin \theta =\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ and $\cos \theta =\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
Now, let us come back to the ellipse and the tangent line, so the slope of the line PM will be same as that of the slope of the line MN because PM is a part of MN, so using the formula $\dfrac{\Delta y}{\Delta x}$ for the slope of the line MN we get,
$\Rightarrow $ Slope of PM = slope of MN = $\dfrac{\left( b\sin \theta -0 \right)}{\left( a\cos \theta -l \right)}$
Substituting the value of the slope equal to -1 we get,
$\begin{align}
  & \Rightarrow -1=\dfrac{\left( b\sin \theta \right)}{\left( a\cos \theta -l \right)} \\
 & \Rightarrow -1\left( a\cos \theta -l \right)=b\sin \theta \\
 & \Rightarrow l-a\cos \theta =b\sin \theta \\
 & \Rightarrow l=b\sin \theta +a\cos \theta \\
\end{align}$
Substituting the values $\sin \theta =\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ and $\cos \theta =\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ we get,
$\begin{align}
  & \Rightarrow l=b\times \dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}+a\times \dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \\
 & \Rightarrow l=\dfrac{{{b}^{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}+\dfrac{{{a}^{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \\
 & \Rightarrow l=\dfrac{{{a}^{2}}+{{b}^{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \\
 & \therefore l=\sqrt{{{a}^{2}}+{{b}^{2}}} \\
\end{align}$
Hence, option (b) is the correct answer.

Note: It is to be noted that whenever the square root of any term is taken, it will always yield two results, the positive and negative counterparts of the same number. But we know that length cannot be zero therefore, we only consider the positive root of the term. The general equation of an ellipse should be remembered which is $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{\left( y-k \right)}{{{b}^{2}}}=1$.