Question

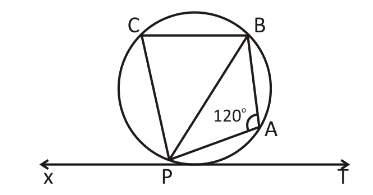
If $ \angle BAP = 120^\circ $ Find $ \angle BPT $
A. $ 120^\circ $
B. $ 80^\circ $
C. $ 50^\circ $
D. $ 60^\circ $

Answer 1

Hint: Here, we are going to use the concept of the cyclic quadrilateral the Tangent –chord theorem which states that in any circle the angle between the chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment.

Complete step-by-step answer:
From the given figure, we can observe that the quadrilateral ABCP is the cyclic quadrilateral as all the vertices of the quadrilateral on the circumference of the circle.
Since, the opposite angles in the quadrilateral are supplementary; the sum of two angles is equal to $ 180^\circ $
 \[\angle BAP + \angle PCB = 180^\circ \]
Place the known value in the above equation-
 \[120^\circ + \angle PCB = 180^\circ \]
Make the required angle the subject –
 \[\angle PCB = 180^\circ - 120^\circ \]
Simplify the above equation –
 \[\angle PCB = 60^\circ \]
By, using the Tangent –chord theorem which states that in any circle the angle between the chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment.
 $ \Rightarrow \angle PCB = \angle BPT $
Since, we have the value of \[\angle PCB = 60^\circ \] placed in the above equation.
 $ \Rightarrow \angle PCB = \angle BPT = 60^\circ $
Therefore, the required measure of $ \angle BPT = 60^\circ $
So, the correct answer is “ $ \angle BPT = 60^\circ $ ”.

Note: Remember the properties of the cyclic quadrilaterals and apply accordingly which states that the opposite angles of a cyclic quadrilateral are supplementary and if one side of a cyclic quadrilateral are produced then the exterior angle will be equal to the opposite interior angle. Also, note that if the sum of any pair of opposite angles of a quadrilateral is $ 180^\circ $ then the given quadrilateral is the cyclic quadrilateral.