Question

If a man of height $6$ft walks at a uniform speed of $9$ft/sec from a lamp of height $15$ft then the length of his shadow is increasing at the rate of
(A)$6$ft/sec
(B)$12$ft/sec
(C)$10$ft/sec
(D)$15$ft/sec

Answer 1

Hint: First of all, we have to find the length of shadow (say$x$) and then apply following formula to find the rate of increase of length of shadow, i.e., speed of shadow (${v_s}$):
${v_s} = \dfrac{{dx}}{{dt}}$

Complete step-by-step answer:
Given, height of a man= $6$ft
Speed of man= $9$ft/sec
Height of lamp= $15$ft
We have to calculate the rate of increase of length of shadow, i.e., speed of shadow (${v_s}$).
After ‘$t$’sec, the man would move a distance of $9t$ ft away from the lamp. Let the shadow move a distance of $x$ft in ‘$t$’sec.

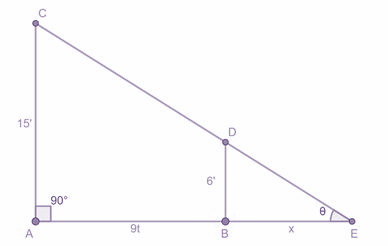
Consider $\Delta AEC$ and $\Delta BED$;
$\angle AEC = \angle BED = \theta $ (common angle)
$\angle EAC = \angle EBD = {90^ \circ }$
$\therefore $$\Delta AEC \sim \Delta BED$ (By AA criteria of similarity of triangles)
We know that if two triangles are similar then their corresponding sides are in the same ratio.
$\therefore \dfrac{{AC}}{{BD}} = \dfrac{{AE}}{{BE}}$
On substituting the values, we get-
$\dfrac{{15}}{6} = \dfrac{{9t + x}}{x}$
On simplifying it, we get-
$ \Rightarrow 15x = 54t + 6x$
$ \Rightarrow 15x - 6x = 54t$
$ \Rightarrow 9x = 54t$
$ \Rightarrow x = \dfrac{{54t}}{9}$
$ \Rightarrow x = 6t$ ….. (1)
As we know that the derivative of displacement$\left( x \right)$ with respect to time $\left( t \right)$ gives us the velocity.
Therefore, velocity of shadow, ${v_s} = \dfrac{{dx}}{{dt}}$
$ \Rightarrow {v_s} = \dfrac{d}{{dt}}\left( {6t} \right)$
$ \Rightarrow {v_s} = 6$ ft/sec
Therefore, the length of shadow is increasing at the rate of $6$ft/sec.
So, option (A) is the correct answer.

Note: Here we use AA (Angle-Angle) criteria of similarity which states that if two corresponding angles of two triangles are equal, then two triangles are similar. Also, similar triangles have a property that their corresponding sides are in the same ratio.