Question

If A is the area of triangle formed by positive x axis and the normal and the tangent to the circle ${{x}^{2}}+{{y}^{2}}=4$ at $\left( 1,\sqrt{3} \right)$ . then $\dfrac{A}{\sqrt{3}}$ is equal to.

Answer 1

Hint: We know that the centre of circle is origin and the normal of circle always passes through origin. Now we have two vertices of triangle one is origin and other is $\left( 1,\sqrt{3} \right)$ . Now we will find its third vertex. We will first find the equation of tangent by differentiating the equation of circle and then using slope point form. Once we have equation of tangent we will find the coordinate where it cuts x axis this is our third vertex. Now Area of right angle triangle is $\dfrac{1}{2}\times base\times height$ Hence we can easily find the area of triangle

Complete step by step answer:
Now first consider the equation of circle ${{x}^{2}}+{{y}^{2}}=4$ .
This is a circle passing with centre $(0,0)$ and radius 4.
Now let us differentiate the equation of circle
Hence we get
$\begin{align}
  & 2x+2y\dfrac{dy}{dx}=0 \\
 & \Rightarrow 2y\dfrac{dy}{dx}=-2x \\
 & \Rightarrow \dfrac{dy}{dx}=\dfrac{-2x}{2y} \\
 & \Rightarrow \dfrac{dy}{dx}=-\dfrac{x}{y} \\
\end{align}$
Now this is $\dfrac{dy}{dx}$ is nothing but slope of tangent at point $\left( x,y \right)$ .
Let us call the point $\left( 1,\sqrt{3} \right)$ as B
Hence at point $B:\left( 1,\sqrt{3} \right)$ the slope of tangent is $\dfrac{dy}{dx}=\dfrac{-\sqrt{3}}{1}$
Now the equation of line passing through point $\left( {{x}_{1}},{{y}_{1}} \right)$ and slope m is given by.
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Hence the equation of line passing through $\left( 1,\sqrt{3} \right)$ the slope of tangent is $\dfrac{dy}{dx}=\dfrac{-\sqrt{3}}{1}$ is given by
$\begin{align}
  & y-\sqrt{3}=\left( -\sqrt{3} \right)\left( x-1 \right) \\
 & \Rightarrow y-\sqrt{3}=-\sqrt{3}x+\sqrt{3} \\
 & \Rightarrow y+\sqrt{3}x=2\sqrt{3} \\
\end{align}$
Now also we know that the normal of circle passes through centre of circle
Hence we have the normal at B passes through origin
Now let us say O is origin and the tangent at B cuts x-axis at A
So now we need to find the area of ΔOAB
Now consider the diagram

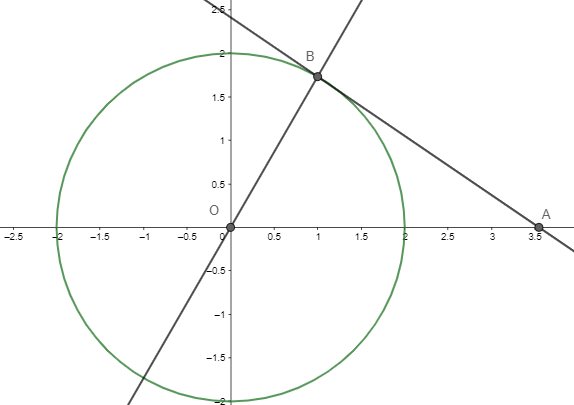
Now we know that coordinates of O are (0, 0).
Coordinates of B are $\left( 1,\sqrt{3} \right)$
Let us try to find coordinates of A.
Now A lies on the tangent $y+\sqrt{3}x=2\sqrt{3}$ and a also lies on x axis
Hence by putting y = 0, we get x coordinate of A
$\begin{align}
  & 0+\sqrt{3}x=2\sqrt{3} \\
 & \Rightarrow x=2 \\
\end{align}$
Hence coordinate of A is (2, 0)
We know that normal is perpendicular to tangent.
Now since OB is normal and AB is tangent angle B = 90°
Now area of right angle triangle is $\dfrac{1}{2}\times \left( base \right)\times \left( height \right)$
Hence area of triangle ABO = $\dfrac{1}{2}\times \left( AB \right)\times \left( OB \right).................(1)$
Now distance between two points is given by $\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
We know that $A=(2,0),B=(1,\sqrt{3})$ and $O=(0,0)$
Hence $OA=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}=\sqrt{4}=2............(2)$
And $OB=\sqrt{{{\left( 0-1 \right)}^{2}}+{{\left( 0-\sqrt{3} \right)}^{2}}}=\sqrt{4}=2............(3)$
From equation (1), equation (2) and equation (3) we get
Area of triangle formed $=\dfrac{1}{2}\times 2\times 2=2$
Hence the area of triangle is 2 sq units.
Hence we have $\dfrac{A}{\sqrt{3}}=\dfrac{2}{\sqrt{3}}$
Note:
We have that tangent is always perpendicular to radius of circle. Also Normal is defined as the line perpendicular to tangent. Hence the normal is always along radius and hence passes through center.