Question

If A, B and C are mutually exclusive and exhaustive events of a random experiment such that \[P\left( B \right)=\dfrac{3}{2}P\left( A \right)\ and\ P\left( C \right)=\dfrac{1}{2}P\left( B \right)\], then \[P\left( A\cup C \right)=\]
A. $\dfrac{3}{13}$
B. $\dfrac{6}{13}$
C. $\dfrac{7}{13}$
D. $\dfrac{10}{13}$

Answer 1

Hint: We will first start by using the fact that mutually exclusive and exhaustive events means that if A and B are two such events then $P\left( A \right)+P\left( B \right)=1\ and\ P\left( A\cap B \right)=\phi $. Also, we will use the data given in question to find the value of each event by forming an equation with the help of fact that events are mutually exclusive and exhaustive.

Complete step-by-step answer:
Now, before starting the solution we have to first understand that mutually exclusive and exhaustive events mean that if there are three events A, B and then at least one of them must occur and probability of occurring more than one event is \[\phi \],we can also describe it as that their union must cover all the events within the entire sample space i.e. $A\cup B\cup C=S\ \text{and }P\left( A\cap B \right)=\phi , P\left( B\cap C \right)=\phi ,P\left( C\cap A \right)=\phi $
Now, we have been given three mutually exclusive and exhaustive events A, B, C.

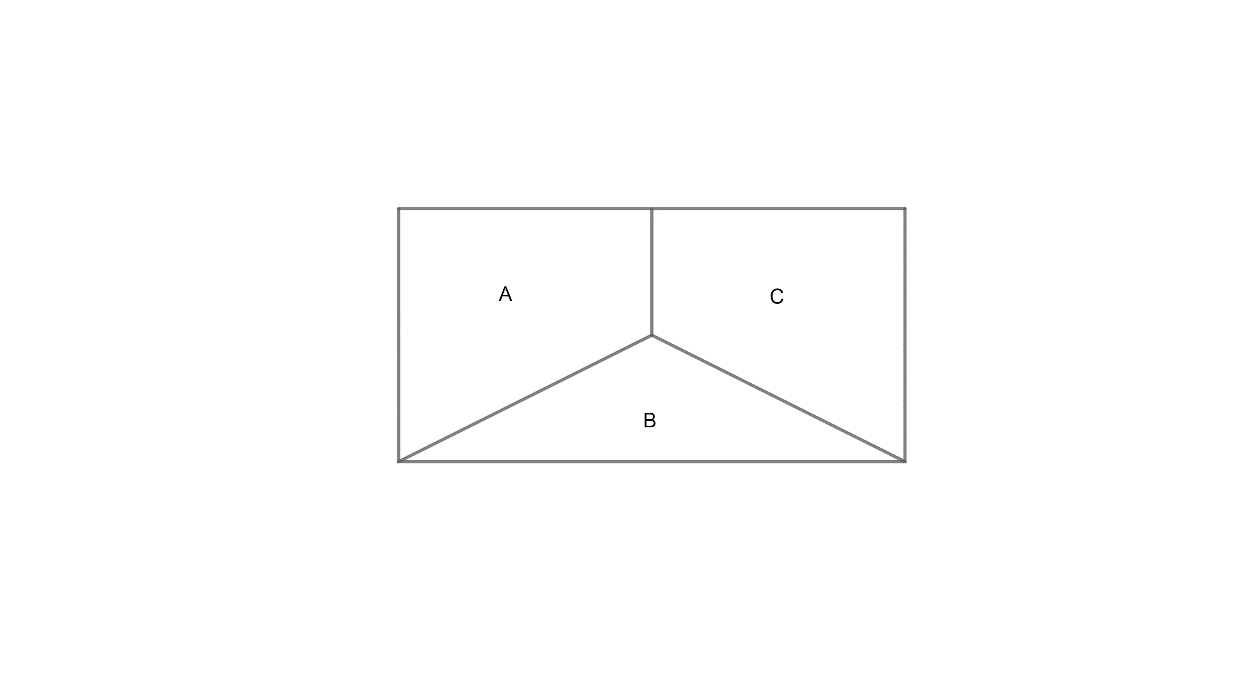
Now, we have given that,
$\begin{align}
  & P\left( B \right)=\dfrac{3}{2}P\left( A \right)............\left( 1 \right) \\
 & P\left( C \right)=\dfrac{1}{2}P\left( B \right)............\left( 2 \right) \\
\end{align}$
Now, substituting P(B) from (1) in (2) we have;
$\begin{align}
  & P\left( C \right)=\dfrac{1}{2}\left( \dfrac{3}{2}P(A) \right) \\
 & P\left( C \right)=\dfrac{3}{4}P\left( A \right)............\left( 3 \right) \\
\end{align}$
Now, we know that if A, B, C are mutually exclusive and exhaustive events then,
$P\left( A \right)+P\left( B \right)+P\left( C \right)=1$
Now, using (2) and (3) we have;
$\begin{align}
  & P\left( A \right)+\dfrac{3}{2}P\left( A \right)+\dfrac{3}{4}P\left( A \right)=1 \\
 & \dfrac{4P\left( A \right)+6P\left( A \right)+3P\left( A \right)}{4}=1 \\
 & 13P\left( A \right)=4 \\
 & P\left( A \right)=\dfrac{4}{13}...........\left( 4 \right) \\
\end{align}$
Now, we have to find the value of $P\left( A\cup C \right)$. Since, the events are mutually exclusive and exhaustive therefore,
$P\left( A\cup C \right)=P\left( A \right)+P\left( C \right)$
Now, from (3) and (4) we have,
$\begin{align}
  & P\left( A\cup C \right)=\dfrac{4}{13}+\dfrac{3}{4}\times \dfrac{4}{13} \\
 & =\dfrac{4}{13}+\dfrac{3}{13} \\
 & P\left( A\cup C \right)=\dfrac{7}{13} \\
\end{align}$
Hence, the correct option is C.

Note: It is important to note that we have used secular properties of mutually exclusive and exhaustive events. For example, if A, B, C are such events then,
$\begin{align}
  & P\left( A+B+C \right)=1 \\
 & P\left( A\cap B \right)=P\left( B\cap C \right)=P\left( B\cap A \right)=\phi \\
\end{align}$
Hence, it is important to remember these to solve the question easily.