Question

How many degrees are in a triangle?

Answer 1

Hint: When we draw a polygon, we see that it has many vertices; and depending on the number of sides in the polygon, we give different names to differently shaped polygons. A polygon having three sides is known as a triangle, the angle between adjacent sides of the polygon is called the interior angle. A triangle has three interior angles. In the given question, we will find out the measure of each interior angle by some constructions and prove that their sum is equal to 180 degrees.

Complete step-by-step solution:
We have to prove that the sum of all the interior angles present in a triangle is 180 degrees. It can be done as follows –
Draw a line “m” through the vertex A parallel to the side BC.

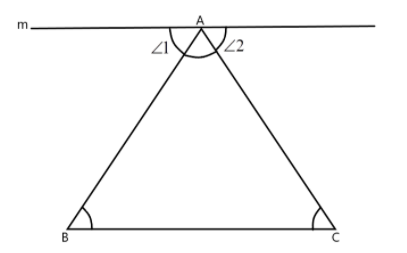
We see that $\angle 1$ , $\angle BAC$ and $\angle 2$ lie on the straight line “m”. so the sum of these three angles is equal to 180 degrees –
$\angle 1 + \angle BAC + \angle 2 = 180^\circ $
Now, line “m” is parallel to line BC. So –
$\angle 1 = \angle ABC$ and $\angle 2 = \angle ACB$ (alternate interior angles)
Using these two values in the above equation, we get –
$\angle ABC + \angle BAC + \angle ACB = 180^\circ $
Hence proved that the sum of all the interior angles of any triangle is 180 degrees.

Note: The lines that when extended to infinity do not intersect at any point, these lines have certain properties. For example, we have used their property of alternate interior angles, according to which the angles lying between the inner corners of the parallel lines and the slanting line (transversal) that cuts the two lines are equal, the angles lie on the opposite side of the transversal.