Question

How do you solve\[\;4x + 7 = 13?\]

Answer 1

Hint: In this question we have to find the $x$ value from the above algebraic equation. For that we are going to simplify the equation. Next, we rearrange the variables and numbers. And also we are going to add and subtraction in complete step by step solution.Here, Algebra is a branch of mathematics dealing with symbols and the rules for manipulating those symbols. In elementary algebra, those symbols represent quantities without fixed values, known as variables. The letters $x$ and $y$ represent the areas of the field.

Complete step by step answer:
Given:
\[ \Rightarrow \;4x + 7 = 13\]
To solve this, we need to get the variable x by itself. To do so, let's move everything else to the other side of the equation:
First, subtract both sides by 7 and we get
\[ \Rightarrow 4x + 7\;\; - \;\;7 = 13\;\; - \;\;7\]
Next, cancel opposite sign in the left hand side and we get
\[ \Rightarrow 4x = 6\]
Now divide both sides by 4 and we get
$ \Rightarrow \dfrac{{4x}}{4} = \dfrac{6}{4}$
On simplify we get,
$ \Rightarrow \dfrac{{\not{4}x}}{{\not{4}}} = \dfrac{6}{4}$
Then we get,
$ \Rightarrow x = \dfrac{6}{4}$
Divide numerator and denominator by 2 and we get
$ \Rightarrow x = \dfrac{{6 \div 2}}{{4 \div 2}}$
$ \Rightarrow x = \dfrac{3}{2}{\text{ }}or{\text{ }}1.5$
This is the required answer.
Graph of given equation:

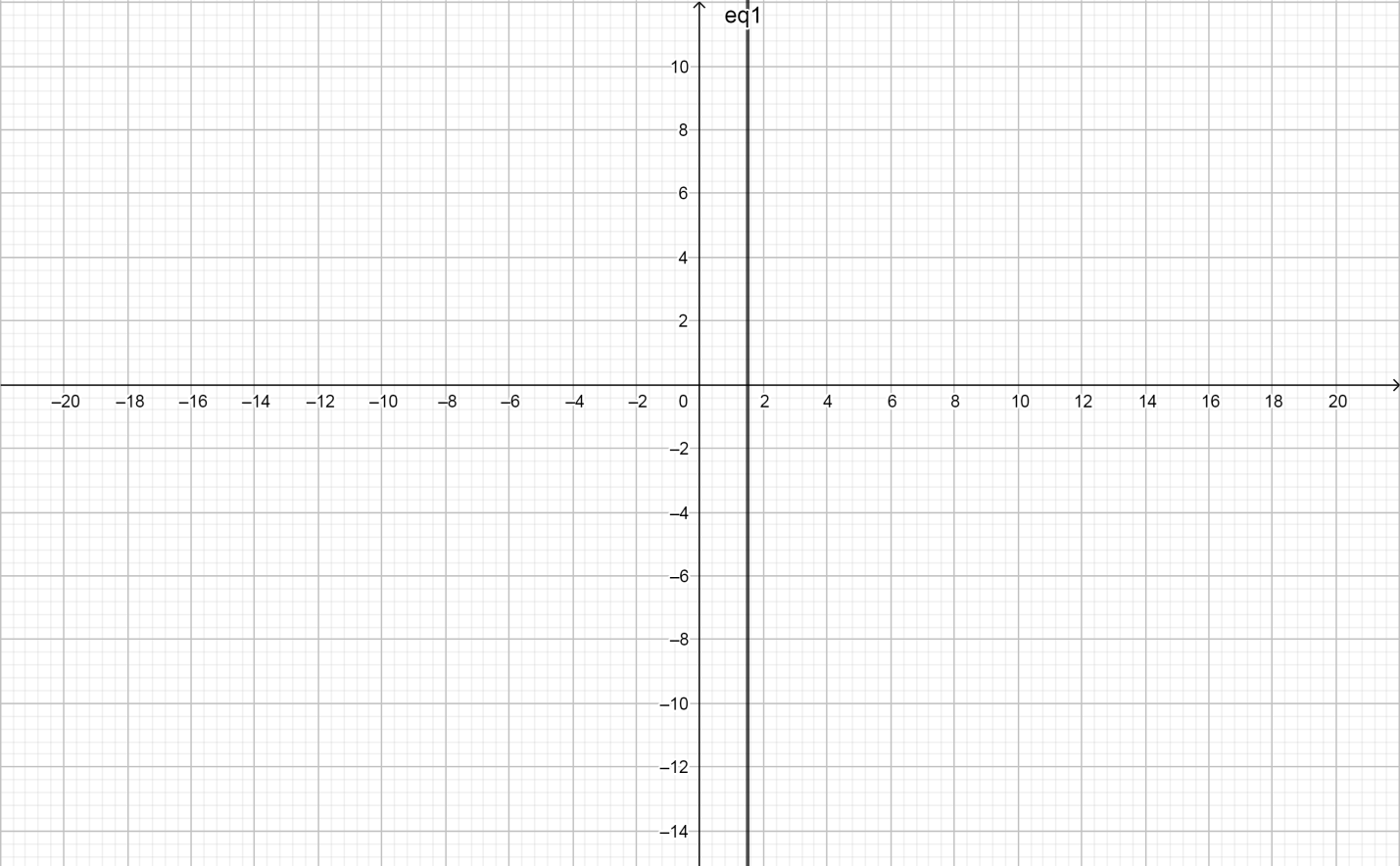
Note: The students remember only the basics of the algebra equation. The basic of algebra equation is nothing but the simple operation of mathematics like addition, subtraction, multiplication, and division involving both constant as well as variable. For example, $x + 10 = 0$.
A linear inequality looks exactly like a linear equation, with the inequality sign replacing the equality sign. Linear inequalities are the expressions where any two values compared by the inequality symbols such as $' < ',' > ',' \leqslant 'or' \geqslant '.$
There is another little hard way to find the answer.
Given:
\[ \Rightarrow \;4x + 7 = 13\]
Move the number 7 right hand side of the above equation and we get
\[ \Rightarrow \;4x = 13 - 7\]
Now subtract the right hand side and we get
\[ \Rightarrow \;4x = 6\]
Next move the number 4 and we get
$ \Rightarrow x = \dfrac{6}{4}$
Divide the above equation and we get
$ \Rightarrow x = \dfrac{{{{\not{6}}^3}}}{{{{\not{4}}^2}}}$
$ \Rightarrow x = \dfrac{3}{2}{\text{ }}or{\text{ }}1.5$
This is the required answer.