Question

How do you solve $3x - 8 = 2$?

Answer 1

Hint: First step is to isolate the variable terms on one side by performing the same mathematical operations on both sides of the equation. Next step is to isolate the constant terms on the other side by performing the same mathematical operations on both sides of the equation. Next step is to make the coefficient of the variable equal to $1$ using multiplication or division property.

Complete step by step solution:
The algebraic equation is $3x - 8 = 2$.
We have to find the value of $x$.
First step is to isolate the variable terms on one side by performing the same mathematical operations on both sides of the equation.
Here, the variable term $x$ is already on one side of the equation.
Thus, $3x - 8 = 2$.
Next step is to isolate the constant terms on the other side by performing the same mathematical operations on both sides of the equation.
So, adding $8$ to both sides of the equation $3x - 8 = 2$.
$ \Rightarrow 3x - 8 + 8 = 2 + 8$
It can be written as
$ \Rightarrow 3x = 10$
Next step is to make the coefficient of the variable equal to $1$ using multiplication or division property.
So, divide both sides of the equation by $3$, we get
$ \Rightarrow \dfrac{{3x}}{3} = \dfrac{{10}}{3}$
Cancel the common factor.
$\therefore x = \dfrac{{10}}{3}$

Therefore, $x = \dfrac{{10}}{3}$ is the solution of $3x - 8 = 2$.

Note:
An algebraic equation is an equation involving variables. It has an equality sign. The expression on the left of the equality sign is the Left Hand Side (LHS). The expression on the right of the equality sign is the Right Hand Side (RHS).

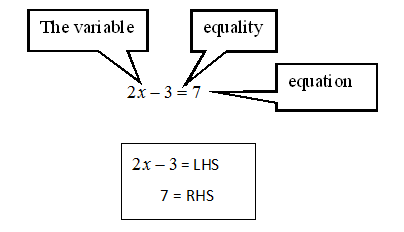
In an equation the values of the expressions on the LHS and RHS are equal. This happens to be true only for certain values of the variable. These values are the solutions of the equation.