Question

How do you graph $y = \left| {2x + 5} \right|$?

Answer 1

Hint:
To solve this question, we need to find certain points first. First and the foremost, we will find the absolute value vertex. After that, we will decide the domain of the given function. And at last we will find a few points on the graph by taking some different values of variable $x$.

Complete step by step solution:
We are given the function $y = \left| {2x + 5} \right|$.
First we will find the absolute value vertex. For this first we will find the x-coordinate of the vortex by equating the inside of the absolute to zero.
$2x + 5 = 0 \Rightarrow x = - \dfrac{5}{2}$
Now we will find the y-coordinate by putting the value of $x = - \dfrac{5}{2}$.
$
  y = \left| { - \dfrac{5}{2} + 5} \right| \\
   \Rightarrow y = \left| {\dfrac{5}{2}} \right| = \dfrac{5}{2} \\
 $
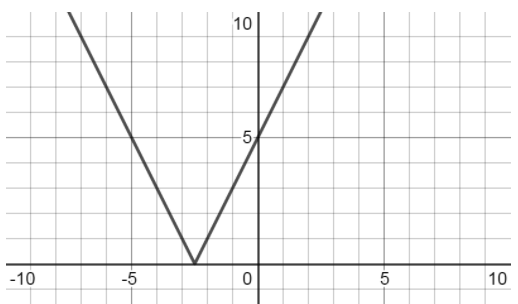
Thus, the absolute vertex for the function $y = \left| {2x + 5} \right|$ is $\left( { - \dfrac{5}{2},\dfrac{5}{2}} \right)$.
The domain of the expression is all real numbers except where the expression is undefined. In our case, there is no real number that makes the expression undefined.
Now, we will find some points to plot the graph.
Let us find the point where the value of $x = - 5$.
$y = \left| {2x + 5} \right| = \left| { - 10 + 5} \right| = \left| 5 \right| = 5$
Thus we get one point on the graph as $\left( { - 5,5} \right)$.
Let us find the point where the value of $x = - 1$.
$y = \left| {2x + 5} \right| = \left| { - 2 + 5} \right| = \left| 3 \right| = 3$
Thus we get one point on the graph as $\left( { - 1,3} \right)$.
Let us find the point where the value of $x = 0$.
$y = \left| {2x + 5} \right| = \left| {0 + 5} \right| = \left| 5 \right| = 5$
Thus we get one point on the graph as $\left( {0,5} \right)$.
Let us find the point where the value of $x = 1$.
$y = \left| {2x + 5} \right| = \left| {2 + 5} \right| = \left| 7 \right| = 7$
Thus we get one point on the graph as $\left( {1,7} \right)$.
From this information we can plot the graph of the function $y = \left| {2x + 5} \right|$as:

Note:
Here, we have seen that the given function $y = \left| {2x + 5} \right|$ can be defined for all the real numbers. Therefore its domain can be written in the interval form as $\left( { - \infty ,\infty } \right)$. Also in the form of a set we can say that this function is defined for \[\{ x/x \in R\} \].