Question

How do you graph $r=4\sin \left( 2\theta \right)$?

Answer 1

Hint: The given equation is a relation between the polar coordinates $r$ and $\theta $. We have to convert them to the rectangular coordinates $x$ and $y$ using the equations $x=r\cos \theta $ and $y=r\sin \theta $. Then, we will have to check for the symmetries with respect to the coordinate axes by replacing $x$ by $-x$ and $y$ by $-y$ on by one. Also, we have to check if the curve passes through the origin by checking if $\left( 0,0 \right)$ satisfies the equation. If the curve passes through the origin, then we can obtain the equation of the tangent to the curve at the origin by equating the lowest degree term of the equation to zero. With all these points we can sketch the required graph.

Complete step-by-step solution:
The equation given in the question is
$r=4\sin \left( 2\theta \right)$
Putting the trigonometric identity $\sin \left( 2\theta \right)=2\sin \theta \cos \theta $ in the above equation we get
$\begin{align}
  & \Rightarrow r=4\left( 2\sin \theta \cos \theta \right) \\
 & \Rightarrow r=8\sin \theta \cos \theta .........(i) \\
\end{align}$
We know that $r$ and $\theta $ are the polar coordinates. So firstly we need to convert it into the Cartesian equation by using the relations between the rectangular and the polar coordinates which are given by
$\begin{align}
  & \Rightarrow x=r\cos \theta \\
 & \Rightarrow \cos \theta =\dfrac{x}{r}........(ii) \\
\end{align}$
Also
$\begin{align}
  & \Rightarrow y=r\sin \theta \\
 & \Rightarrow \sin \theta =\dfrac{y}{r}.........(iii) \\
\end{align}$
Putting (ii) and (iii) in (i) we get
\[\begin{align}
  & \Rightarrow r=8\left( \dfrac{x}{r} \right)\left( \dfrac{y}{r} \right) \\
 & \Rightarrow r=\dfrac{8xy}{{{r}^{2}}} \\
 & \Rightarrow {{r}^{3}}=8xy \\
\end{align}\]
Now, we also know that $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$. Putting this above, we get
$\begin{align}
  & \Rightarrow {{\left( \sqrt{{{x}^{2}}+{{y}^{2}}} \right)}^{3}}=8xy \\
 & \Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{\dfrac{3}{2}}}=8xy \\
\end{align}$
On squaring both the sides, we get
$\begin{align}
  & \Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{3}}={{\left( 8xy \right)}^{2}} \\
 & \Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{3}}=64{{x}^{2}}{{y}^{2}} \\
 & \Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{3}}-64{{x}^{2}}{{y}^{2}}=0........(iv) \\
\end{align}$
This is our Cartesian equation. For sketching the curve, we check the below points:
(i) Symmetry: We replace $x$ by $-x$ in (iv) to get
$\begin{align}
  & \Rightarrow {{\left( {{\left( -x \right)}^{2}}+{{y}^{2}} \right)}^{3}}-64{{\left( -x \right)}^{2}}{{y}^{2}}=0 \\
 & \Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{3}}-64{{x}^{2}}{{y}^{2}}=0 \\
\end{align}$
So the equation remains unchanged after replacing $x$ by $-x$. This means that the given curve is symmetric with respect to the y-axis.
Similarly we can prove the curve to be symmetric about the x-axis.
(ii) Origin: Substituting $x=0$ and $y=0$ in (iv), we get
\[\begin{align}
  & \Rightarrow {{\left( {{0}^{2}}+{{0}^{2}} \right)}^{3}}-64{{\left( 0 \right)}^{2}}{{\left( 0 \right)}^{2}}=0 \\
 & \Rightarrow 0=0 \\
\end{align}\]
The LHS is equal to the RHS, this means that the curve must pass through the origin.
(iii) Tangent at origin: For getting the equation of tangent at the origin, we substitute the least degree term equal to zero. In the equation (iv) we can observe that the least degree term is $-64{{x}^{2}}{{y}^{2}}$. Therefore, we equate it to zero to get
$\Rightarrow -64{{x}^{2}}{{y}^{2}}=0$
On solving, we get
$x=0$ and $y=0$
These are respectively the equations of the y-axis and the x-axis. So the coordinate axes are the tangents to the given curve.
With all the information above, we can sketch the graph of the given curve as

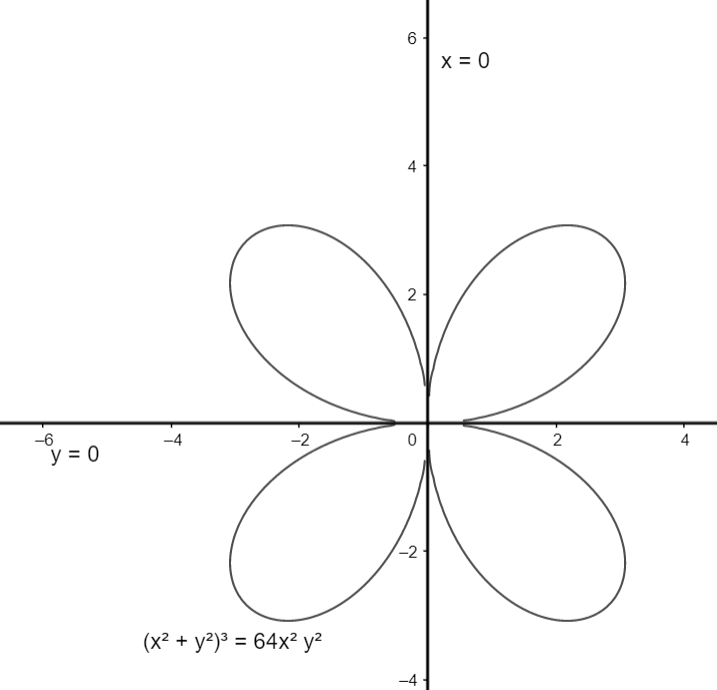
Hence, we have graphed $r=4\sin \left( 2\theta \right)$.

Note: We can solve this question without converting the given polar equation to the Cartesian equation. For this, we have to enlist the values of $r$, the distances from the origin, for various values of the angle $\theta $. We have to consider a particular range of different angles for each of the four quadrants. But the method of sketching the curve from the Cartesian equation is easier.