Question

How do you graph and list the amplitude, period, phase shift for \[y=-\cos 2x-5\]?

Answer 1

Hint: Upon comparing the given wave equation with the standard cosine equation, we will obtain the values of the variables used in the equation. Using these values of the variables we can compute the values of the amplitude, period, phase shift and even the vertical shift.

Complete step-by-step answer:
Consider the standard equation of the cosine function.
\[y=a\cos (bx+c)+d\]
Here, a, b, c and d are the variables and x and y are the axes.
The formula for computing the amplitude of the cosine wave function is given as follows.
\[A=|a|\]
 The formula for computing the period of the cosine wave function is given as follows.
\[T=\dfrac{2\pi }{b}\]
The formula for computing the phase shift of the cosine wave function is given as follows.
\[\phi =-\dfrac{c}{b}\]
The formula for computing the vertical shift of the cosine wave function is given as follows.
\[\text{Vertical shif}t=d\]
From the given information, we have the data as follows.
The wave equation: \[y=-\cos 2x-5\]
Compare the given wave equation with the standard wave equation. So, we have,
\[\begin{align}
  & y=a\cos (bx+c)+d\Leftrightarrow y=-\cos 2x-5 \\
 & \Rightarrow a=-1 \\
 & \Rightarrow b=2 \\
 & \Rightarrow c=0 \\
 & \Rightarrow d=-5 \\
\end{align}\]
We have obtained the values of the variables to find the value of the properties of the wave, such as the amplitude, the phase shift, the period and the vertical shift.
The formula for computing the amplitude of the cosine wave function is given as follows.
\[\begin{align}
  & A=|a| \\
 & \Rightarrow A=|-1| \\
 & \therefore A=1 \\
\end{align}\]
 The formula for computing the period of the cosine wave function is given as follows.
\[\begin{align}
  & T=\dfrac{2\pi }{b} \\
 & \Rightarrow T=\dfrac{2\pi }{2} \\
 & \therefore T=\pi \\
\end{align}\]
The formula for computing the phase shift of the cosine wave function is given as follows.
\[\begin{align}
  & \phi =-\dfrac{c}{b} \\
 & \Rightarrow \phi =-\dfrac{0}{2} \\
 & \therefore \phi =0 \\
\end{align}\]
The formula for computing the vertical shift of the cosine wave function is given as follows.
\[\begin{align}
  & \text{Vertical shif}t=d \\
 & \therefore \text{Vertical shif}t=-5 \\
\end{align}\]
The graph of wave equation \[y=-\cos 2x-5\]is given as follows.

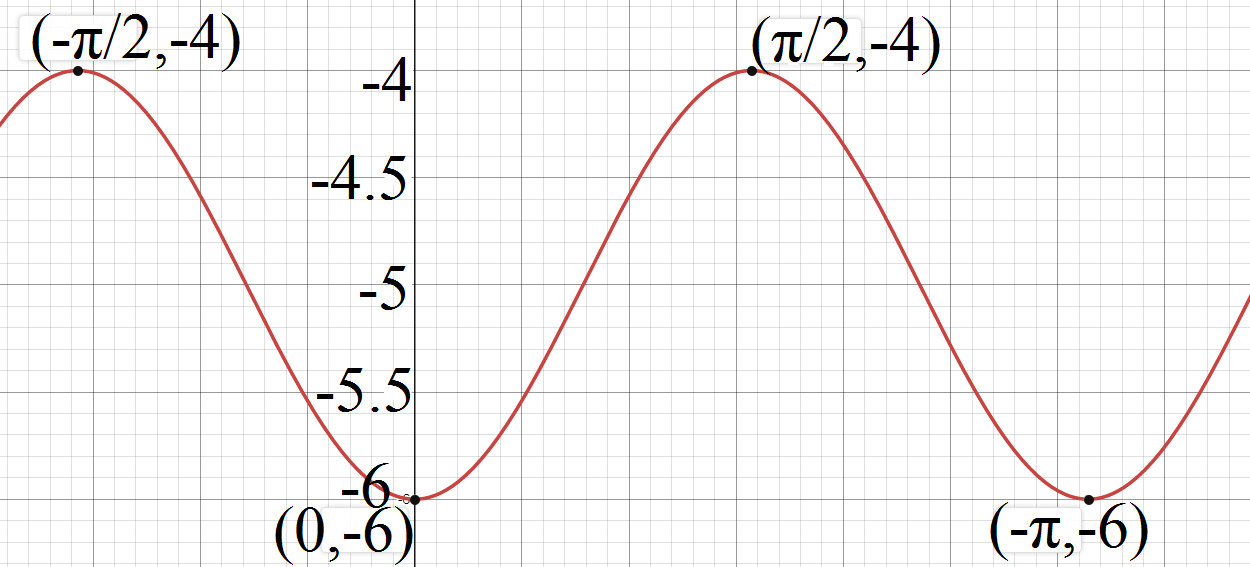
From the graph, it’s clear that the amplitude of the given wave is1, but, because of the vertical shift of -5, the amplitude of the wave changes to -4.
\[\therefore \] The amplitude, period, phase shift for\[y=-\cos 2x-5\] are 1, \[\pi \]and 0.

Note: The vertical shift is related to the amplitude of the wave. If the value of the vertical shift is positive, then, we have to add that value with the amplitude of the wave, in case, if the value of the vertical shift is negative, then, we have to subtract that value from the amplitude of the wave. In our case, we have subtracted 5 from 1.