Question

Given the electric field in the region E=2x$\hat{i}$, find the net electric flux through the cube and the charge enclosed by it.

Answer 1

Hint: Electric flux is the rate of flow of electric field through a closed surface. In the given cubic surface which is closed we need to find the electric flux from the electric field, which can be calculated by a simple formula. The dot product of the electric field with the area enclosed gives us the electric flux.

Formula used:
The electric flux, \[\phi \] = E.A

Complete answer:
Given,
Length of side of the cube = a
Electric Field = E=2x$\hat{i}$
The electric field given to us has only x component, so the flux will be present only in the x direction. To calculate the flux, we need to find the area of the region through which flux is flowing.

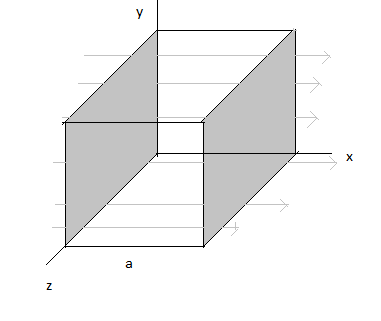
      Fig: diagram showing electric field lines passing through the shaded regions in the x direction

The area of one side of the cube with side a = ${{a}^{2}}$
The electric flux is given by the dot product of electric field and area of the enclosed surface of the cube.
The electric flux through the 2 surfaces of the cube with side a, \[\phi \] =E.A
 =2x${{a}^{2}}$
=2(a)${{a}^{2}}$
=2\[{{a}^{3}}\]
Thus the electric flux in the region is given by 2${{a}^{3}}$

Additional Information:
Although electric fields cannot flow on their own, flux is the way of describing the electric field strength at any distance from the charge which causes the field. The Gauss law of Maxwell’s equation gives the relation between electric flux and charge. As electric flux exists in electrostatics, in electromagnetism, there is the existence of magnetic flux.

Note:
In this problem, we must keep in mind that the flux through the other 4 faces of the cube are 0 since the incoming flux is equal to outgoing flux across those faces in the absence of an electric field and hence the flux cancels to be 0. The area must necessarily be calculated of the region of which flux is calculated.