
How to get the surface area of a cone using integral calculus \[?\]
Answer
568.5k+ views
Hint:This question describes the operation of finding the area of a circle and lateral surface of the cone. We need to know the basic integration and differentiation. Also, we need to know the process of finding\[\sin \theta \], \[\cos \theta \]and \[\tan \theta \]from the triangle.
We need to know trigonometric conditions to make an easy calculation.
Complete step by step solution:
In the given question we have to find the total surface area of a cone using integral calculus. For finding the surface area the following figure will help us,
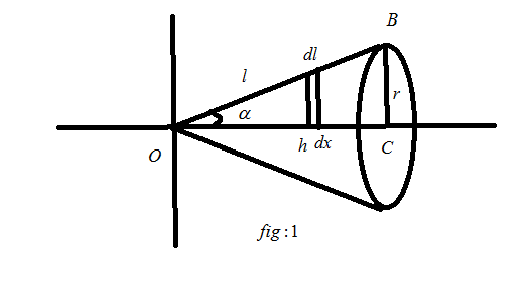
In the above figure,
\[C\] is the center of the bottom of the cone,
\[l\]is the length of slant edge in the cone,
\[h\]is the vertical height of the cone,
\[\alpha \] is the angle between \[OC\]and \[OB\],
\[dl\] is the small part of the slant edge,
\[dx\] is the small part of vertical height,
\[r\]is the radius of the bottom cone.
We know that the bottom of the cone is a circle. So, we have to find the area of the circle. For finding the area of the circle we assume the following figure,
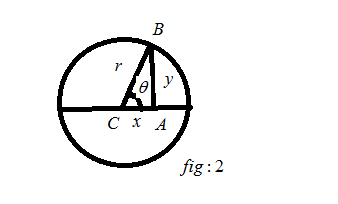
The above figure was drawn with the reference of\[fig:1\]. From the\[fig:2\], we get the following equation
\[{x^2} + {y^2} = {r^2} \to \left( 1 \right)\] (By Pythagoras theorem)
The above equation can also be written as
\[{y^2} = {r^2} - {x^2}\]
\[y = \sqrt {{r^2} - {x^2}} \]
The area of the circle,
\[{A_{circle}}\]=\[\int {\sqrt {{r^2} - {x^2}} } dx\]
Let’s take\[{r^2}\]it as a common term, so we get
\[{A_{circle}} = \int {\sqrt {{r^2}\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \]
We know that\[\sqrt {{r^2}} = r\]
\[{A_{circle}} = r\int {\sqrt {\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \to \left( 2 \right)\]
If we consider the limit between\[ - r\]and\[r\] we can evaluate the area of half of the circle.
From\[fig:2\]we get the following values,
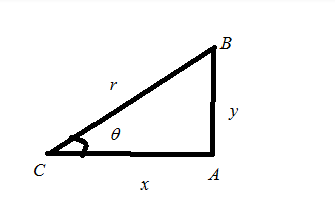
\[
\cos \theta = \dfrac{{adj}}{{opposite}} = \dfrac{x}{r} \\
\dfrac{x}{r} = {\cos ^2}\theta = 1 - {\sin ^2}\theta \\
\]
\[\theta = arc\operatorname{Cos} \left( {\dfrac{x}{r}} \right)\]
Let’s take\[x = - r\]
\[\theta = arc\operatorname{Cos} \left( {\dfrac{{ - r}}{r}} \right)\]
\[\theta = arc\operatorname{Cos} \left( { - 1} \right)\]
We know that, \[arc\operatorname{Cos} ( - 1) = \pi \]
So, \[\theta = \pi \]
Let’s take \[x = r\]
\[\theta = arc\operatorname{Cos} \left( {\dfrac{r}{r}} \right)\]
\[\theta = arc\operatorname{Cos} \left( 1 \right)\]
We know that, \[arc\operatorname{Cos} (1) = 0\]
So, \[\theta = 0\]
We know that,
\[\cos \theta = \dfrac{x}{r}\]
Let’s differentiate the above equation, we get
\[ - \sin \theta d\theta = \dfrac{1}{r}dx\]
So, we get
\[
\dfrac{{dx}}{r} = - \sin \theta d\theta \\
dx = - r\sin \theta d\theta \\
\]
So, the equation\[\left( 2 \right)\]is,
\[{A_{circle}} = r\int {\sqrt {\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \]
(For finding the area of half of the circle the limit will be\[\pi to0\].)
Let’s substitute \[\dfrac{{{x^2}}}{{{r^2}}} = 1 - {\sin ^2}\theta ,dx = - r\sin \theta d\theta \]in the above equation, we get
\[
\dfrac{1}{2}{A_{circle}} = r\int\limits_\pi ^0 {\sqrt {1 - (1 - {{\sin }^2}\theta )} ( - r\sin \theta
d\theta )} \\
\dfrac{1}{2}{A_{circle}} = r\int\limits_\pi ^0 {\sqrt {1 - 1 + {{\sin }^2}\theta } ( - r\sin \theta
d\theta )} \\
\]
Here, \[r\]is constant, so it can be taken to the outside of the interval.
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\sqrt {{{\sin }^2}\theta } (\sin \theta d\theta }
)\]
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\sin \theta .\sin \theta d\theta } \]
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {{{\sin }^2}\theta d\theta } \]
We know that, \[{\sin ^2}\theta = \dfrac{{1 - \cos 2\theta }}{2}\]. So, we get
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\dfrac{{1 - \cos 2\theta }}{2}d\theta } = -
{r^2}\int\limits_\pi ^0 {\left( {\dfrac{1}{2} - \dfrac{{\cos 2\theta }}{2}} \right)d\theta } \]
From equation\[\left( 1 \right)\]
\[{x^2} + {y^2} = {r^2} \to \left( 3 \right)\]
Let’s differentiate the above equation, we get
\[2xdx + 2ydy = 2rdr\]
In the above equation\[r\]is constant so, \[dr = 0\]. So, the above equation becomes,
\[2xdx + 2ydy = 0\]
\[
2xdx = - 2ydy \\
\dfrac{{dy}}{{dx}} = \dfrac{{ - 2x}}{{2y}} = \dfrac{{ - x}}{y} \to \left( 4 \right) \\
\]
From equation\[\left( 1 \right)\]
\[
{y^2} = {r^2} - {x^2} \\
y = \sqrt {{r^2} - {x^2}} \\
\]
By substituting the above-mentioned value in the equation\[\left( 4 \right)\]we get,
\[\dfrac{{dy}}{{dx}} = \dfrac{{ - x}}{{\sqrt {{r^2} - {x^2}} }}\]
The arc length L is
\[L = \int {ds} \]
Here, \[ds = \sqrt {1 + {{\left( {\dfrac{{dy}}{{dx}}} \right)}^2}} dx\]
Let’s substitute the\[\dfrac{{dy}}{{dx}}\]value in the above equation, we get
\[
ds = \sqrt {1 + {{\left( {\dfrac{{ - x}}{{\sqrt {{r^2} - {x^2}} }}} \right)}^2}} dx \\
ds = \sqrt {1 + \dfrac{{{x^2}}}{{{r^2} - {x^2}}}} dx \\
\]
\[
ds = \sqrt {\dfrac{{{r^2} - {x^2} + {x^2}}}{{{r^2} - {x^2}}}} dx \\
ds = \sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} dx \\
\]
Half of the circumference of the circle is given below,
\[L = \int\limits_{ - r}^r {ds} \]
By substituting the value of\[ds\] we get,
\[L = \int\limits_{ - r}^r {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } dx\]
We know that, \[x = r\cos \theta \], \[dx = - r\sin \theta d\theta \]so, the above equation becomes
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } \left( { - r\sin \theta } \right)d\theta
\]
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {{\left( {r\cos \theta } \right)}^2}}}} } \left( { - r\sin \theta } \right)d\theta \]
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2}\left( {1 - {{\cos }^2}\theta } \right)}}} } \left( { - r\sin \theta } \right)d\theta \]
We know that, \[1 - {\cos ^2}\theta = {\sin ^2}\theta \]so, the above equation become,
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2}\left( {{{\sin }^2}\theta } \right)}}} } \left( { - r\sin \theta } \right)d\theta \]
\[L = - r\int\limits_\pi ^0 {\dfrac{1}{{\sin \theta }}} .\sin \theta d\theta \]
\[L = - r\int\limits_\pi ^0 1 d\theta \]
\[
L = - r\left[ \theta \right]_\pi ^0 = - r\left[ {0 - \pi } \right] \\
L = \pi r \\
\]
So, the full circumference of the circle is\[2L = 2\pi r\]
So, the lateral surface area of the cone
\[S = \int\limits_0^h {2\pi f\left( x \right)} dl\]
Here,\[y = f\left( x \right)\]
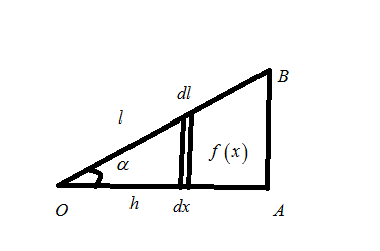
From the given figure
\[
\cos \alpha = \dfrac{h}{l} \\
l = \dfrac{h}{{\cos \alpha }} \\
dl = \dfrac{{dh}}{{\cos \alpha }} = \dfrac{{dx}}{{\cos \alpha }} \\
\tan \alpha = \dfrac{r}{h} = \dfrac{{f\left( x \right)}}{x} \\
\]
\[f\left( x \right) = x\tan \alpha \]
By using the above values we get,
\[S = \int\limits_0^h {2\pi x\tan \alpha \dfrac{{dx}}{{\cos \alpha }}} \]
\[S = 2\pi \dfrac{{\tan \alpha }}{{\cos \alpha }}\int\limits_0^h {xdx} \]
\[
S = 2\pi \dfrac{{\left( {\dfrac{r}{h}} \right)}}{{\left( {\dfrac{h}{l}} \right)}}\left[ {\dfrac{{{x^2}}}{2}}
\right]_0^h \\
S = 2\pi \left( {\dfrac{{rl}}{{{h^2}}}} \right)\left[ {\dfrac{{{h^2}}}{2} - \dfrac{{{0^2}}}{2}} \right]
\\
S = 2\pi r \\
\\
\]
So, the total surface area of the cone\[ = \]total surface area of the circle\[ + \]total surface area of the lateral surface.
The total surface area of the cone=\[\pi {r^2} + 2\pi r\]
Note: We have to consider the bottom of the cone as a circle. At first, we want to find the area of a circle, and next, we want to find the area of the lateral surface. Also, note that the integral of \[\cos \theta \]is\[\sin \theta \] and the differentiation of \[\cos \theta \]is\[ - \sin \theta \]. If a constant term is present inside the integral, we can take the term outside of the integral.
We need to know trigonometric conditions to make an easy calculation.
Complete step by step solution:
In the given question we have to find the total surface area of a cone using integral calculus. For finding the surface area the following figure will help us,

In the above figure,
\[C\] is the center of the bottom of the cone,
\[l\]is the length of slant edge in the cone,
\[h\]is the vertical height of the cone,
\[\alpha \] is the angle between \[OC\]and \[OB\],
\[dl\] is the small part of the slant edge,
\[dx\] is the small part of vertical height,
\[r\]is the radius of the bottom cone.
We know that the bottom of the cone is a circle. So, we have to find the area of the circle. For finding the area of the circle we assume the following figure,
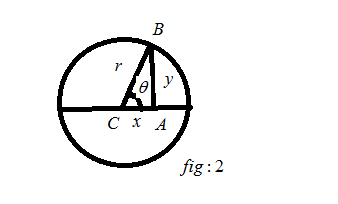
The above figure was drawn with the reference of\[fig:1\]. From the\[fig:2\], we get the following equation
\[{x^2} + {y^2} = {r^2} \to \left( 1 \right)\] (By Pythagoras theorem)
The above equation can also be written as
\[{y^2} = {r^2} - {x^2}\]
\[y = \sqrt {{r^2} - {x^2}} \]
The area of the circle,
\[{A_{circle}}\]=\[\int {\sqrt {{r^2} - {x^2}} } dx\]
Let’s take\[{r^2}\]it as a common term, so we get
\[{A_{circle}} = \int {\sqrt {{r^2}\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \]
We know that\[\sqrt {{r^2}} = r\]
\[{A_{circle}} = r\int {\sqrt {\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \to \left( 2 \right)\]
If we consider the limit between\[ - r\]and\[r\] we can evaluate the area of half of the circle.
From\[fig:2\]we get the following values,

\[
\cos \theta = \dfrac{{adj}}{{opposite}} = \dfrac{x}{r} \\
\dfrac{x}{r} = {\cos ^2}\theta = 1 - {\sin ^2}\theta \\
\]
\[\theta = arc\operatorname{Cos} \left( {\dfrac{x}{r}} \right)\]
Let’s take\[x = - r\]
\[\theta = arc\operatorname{Cos} \left( {\dfrac{{ - r}}{r}} \right)\]
\[\theta = arc\operatorname{Cos} \left( { - 1} \right)\]
We know that, \[arc\operatorname{Cos} ( - 1) = \pi \]
So, \[\theta = \pi \]
Let’s take \[x = r\]
\[\theta = arc\operatorname{Cos} \left( {\dfrac{r}{r}} \right)\]
\[\theta = arc\operatorname{Cos} \left( 1 \right)\]
We know that, \[arc\operatorname{Cos} (1) = 0\]
So, \[\theta = 0\]
We know that,
\[\cos \theta = \dfrac{x}{r}\]
Let’s differentiate the above equation, we get
\[ - \sin \theta d\theta = \dfrac{1}{r}dx\]
So, we get
\[
\dfrac{{dx}}{r} = - \sin \theta d\theta \\
dx = - r\sin \theta d\theta \\
\]
So, the equation\[\left( 2 \right)\]is,
\[{A_{circle}} = r\int {\sqrt {\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \]
(For finding the area of half of the circle the limit will be\[\pi to0\].)
Let’s substitute \[\dfrac{{{x^2}}}{{{r^2}}} = 1 - {\sin ^2}\theta ,dx = - r\sin \theta d\theta \]in the above equation, we get
\[
\dfrac{1}{2}{A_{circle}} = r\int\limits_\pi ^0 {\sqrt {1 - (1 - {{\sin }^2}\theta )} ( - r\sin \theta
d\theta )} \\
\dfrac{1}{2}{A_{circle}} = r\int\limits_\pi ^0 {\sqrt {1 - 1 + {{\sin }^2}\theta } ( - r\sin \theta
d\theta )} \\
\]
Here, \[r\]is constant, so it can be taken to the outside of the interval.
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\sqrt {{{\sin }^2}\theta } (\sin \theta d\theta }
)\]
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\sin \theta .\sin \theta d\theta } \]
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {{{\sin }^2}\theta d\theta } \]
We know that, \[{\sin ^2}\theta = \dfrac{{1 - \cos 2\theta }}{2}\]. So, we get
\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\dfrac{{1 - \cos 2\theta }}{2}d\theta } = -
{r^2}\int\limits_\pi ^0 {\left( {\dfrac{1}{2} - \dfrac{{\cos 2\theta }}{2}} \right)d\theta } \]
From equation\[\left( 1 \right)\]
\[{x^2} + {y^2} = {r^2} \to \left( 3 \right)\]
Let’s differentiate the above equation, we get
\[2xdx + 2ydy = 2rdr\]
In the above equation\[r\]is constant so, \[dr = 0\]. So, the above equation becomes,
\[2xdx + 2ydy = 0\]
\[
2xdx = - 2ydy \\
\dfrac{{dy}}{{dx}} = \dfrac{{ - 2x}}{{2y}} = \dfrac{{ - x}}{y} \to \left( 4 \right) \\
\]
From equation\[\left( 1 \right)\]
\[
{y^2} = {r^2} - {x^2} \\
y = \sqrt {{r^2} - {x^2}} \\
\]
By substituting the above-mentioned value in the equation\[\left( 4 \right)\]we get,
\[\dfrac{{dy}}{{dx}} = \dfrac{{ - x}}{{\sqrt {{r^2} - {x^2}} }}\]
The arc length L is
\[L = \int {ds} \]
Here, \[ds = \sqrt {1 + {{\left( {\dfrac{{dy}}{{dx}}} \right)}^2}} dx\]
Let’s substitute the\[\dfrac{{dy}}{{dx}}\]value in the above equation, we get
\[
ds = \sqrt {1 + {{\left( {\dfrac{{ - x}}{{\sqrt {{r^2} - {x^2}} }}} \right)}^2}} dx \\
ds = \sqrt {1 + \dfrac{{{x^2}}}{{{r^2} - {x^2}}}} dx \\
\]
\[
ds = \sqrt {\dfrac{{{r^2} - {x^2} + {x^2}}}{{{r^2} - {x^2}}}} dx \\
ds = \sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} dx \\
\]
Half of the circumference of the circle is given below,
\[L = \int\limits_{ - r}^r {ds} \]
By substituting the value of\[ds\] we get,
\[L = \int\limits_{ - r}^r {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } dx\]
We know that, \[x = r\cos \theta \], \[dx = - r\sin \theta d\theta \]so, the above equation becomes
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } \left( { - r\sin \theta } \right)d\theta
\]
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {{\left( {r\cos \theta } \right)}^2}}}} } \left( { - r\sin \theta } \right)d\theta \]
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2}\left( {1 - {{\cos }^2}\theta } \right)}}} } \left( { - r\sin \theta } \right)d\theta \]
We know that, \[1 - {\cos ^2}\theta = {\sin ^2}\theta \]so, the above equation become,
\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2}\left( {{{\sin }^2}\theta } \right)}}} } \left( { - r\sin \theta } \right)d\theta \]
\[L = - r\int\limits_\pi ^0 {\dfrac{1}{{\sin \theta }}} .\sin \theta d\theta \]
\[L = - r\int\limits_\pi ^0 1 d\theta \]
\[
L = - r\left[ \theta \right]_\pi ^0 = - r\left[ {0 - \pi } \right] \\
L = \pi r \\
\]
So, the full circumference of the circle is\[2L = 2\pi r\]
So, the lateral surface area of the cone
\[S = \int\limits_0^h {2\pi f\left( x \right)} dl\]
Here,\[y = f\left( x \right)\]

From the given figure
\[
\cos \alpha = \dfrac{h}{l} \\
l = \dfrac{h}{{\cos \alpha }} \\
dl = \dfrac{{dh}}{{\cos \alpha }} = \dfrac{{dx}}{{\cos \alpha }} \\
\tan \alpha = \dfrac{r}{h} = \dfrac{{f\left( x \right)}}{x} \\
\]
\[f\left( x \right) = x\tan \alpha \]
By using the above values we get,
\[S = \int\limits_0^h {2\pi x\tan \alpha \dfrac{{dx}}{{\cos \alpha }}} \]
\[S = 2\pi \dfrac{{\tan \alpha }}{{\cos \alpha }}\int\limits_0^h {xdx} \]
\[
S = 2\pi \dfrac{{\left( {\dfrac{r}{h}} \right)}}{{\left( {\dfrac{h}{l}} \right)}}\left[ {\dfrac{{{x^2}}}{2}}
\right]_0^h \\
S = 2\pi \left( {\dfrac{{rl}}{{{h^2}}}} \right)\left[ {\dfrac{{{h^2}}}{2} - \dfrac{{{0^2}}}{2}} \right]
\\
S = 2\pi r \\
\\
\]
So, the total surface area of the cone\[ = \]total surface area of the circle\[ + \]total surface area of the lateral surface.
The total surface area of the cone=\[\pi {r^2} + 2\pi r\]
Note: We have to consider the bottom of the cone as a circle. At first, we want to find the area of a circle, and next, we want to find the area of the lateral surface. Also, note that the integral of \[\cos \theta \]is\[\sin \theta \] and the differentiation of \[\cos \theta \]is\[ - \sin \theta \]. If a constant term is present inside the integral, we can take the term outside of the integral.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE

Actinoid contraction is more than lanthanoid contraction class 11 chemistry CBSE

The transition element that has lowest enthalpy of class 11 chemistry CBSE

Can anyone list 10 advantages and disadvantages of friction

State the laws of reflection of light




