Question

From the top of a tower h metre high, the angle of depression of two objects, which are in the line with the foot of the tower are $\alpha $ and $\beta $ ($\beta $ > $\alpha $). Find the distance between the two objects.

Answer 1

Hint:We will use the concept of depression to draw the diagram and we will use the trigonometric angular formulas to find the required distance. One of the formulas that we will use here is given by $\tan \left( \theta \right)=\dfrac{\text{perpendicular}}{\text{Base}}$.

Complete step-by-step answer:

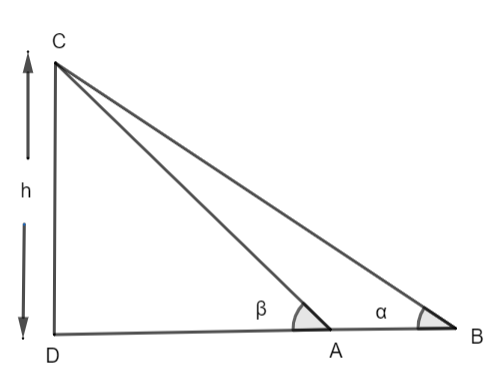
From the figure we get to know that CD represents the tower with height h meter. There are two depressions at point A and B. The angle CAD is angle $\beta $ and angle CBD is the angle $\alpha $.
Here, $\beta $ > $\alpha $ in the figure.
Now, we will apply the formula of trigonometry to find the distance between A and B.
By the formula $\tan \left( \theta \right)=\dfrac{\text{perpendicular}}{\text{Base}}$ we have $\tan \left( \alpha \right)=\dfrac{CD}{BD}$ and $\tan \left( \beta \right)=\dfrac{CD}{AD}$. As we know that CD = h meters.
Therefore, we have $\tan \left( \alpha \right)=\dfrac{h}{BD}$ and $\tan \left( \beta \right)=\dfrac{h}{AD}$.
Also, as BD = AD + BA.
Thus, we get $\tan \left( \alpha \right)=\dfrac{h}{AD+BA}$ and $\tan \left( \beta \right)=\dfrac{h}{AD}$.
Now, we will consider $\tan \left( \alpha \right)=\dfrac{h}{AD+BA}$ which actually results into $\left( AD+BA \right)\tan \left( \alpha \right)=h...(i)$ and $\tan \left( \beta \right)=\dfrac{h}{AD}$ results into $AD\tan \left( \beta \right)=h...(ii)$.
By substituting equation (i) and (ii) we get a new expression as,
$\begin{align}
  & \left( AD+BA \right)\tan \left( \alpha \right)=AD\tan \left( \beta \right) \\
 & \Rightarrow AD\tan \left( \alpha \right)+BA\tan \left( \alpha \right)=AD\tan \left( \beta \right) \\
 & \Rightarrow BA\tan \left( \alpha \right)=AD\tan \left( \beta \right)-AD\tan \left( \alpha \right) \\
 & \Rightarrow BA=\dfrac{AD\tan \left( \beta \right)-AD\tan \left( \alpha \right)}{\tan \left( \alpha \right)}...(iii) \\
\end{align}$
By equation (ii) we get the value of $AD=\dfrac{h}{\tan \left( \beta \right)}$. Now, we will substitute this value in equation (iii).
Therefore we have
 $\begin{align}
  & \Rightarrow BA=\dfrac{AD\tan \left( \beta \right)-AD\tan \left( \alpha \right)}{\tan \left( \alpha \right)} \\
 & \Rightarrow BA=\dfrac{AD\left( \tan \left( \beta \right)-\tan \left( \alpha \right) \right)}{\tan \left( \alpha \right)} \\
 & \Rightarrow BA=\left( \dfrac{h}{\tan \left( \beta \right)} \right)\dfrac{\left( \tan \left( \beta \right)-\tan \left( \alpha \right) \right)}{\tan \left( \alpha \right)} \\
 & \Rightarrow BA=\dfrac{h\left( \tan \left( \beta \right)-\tan \left( \alpha \right) \right)}{\tan \left( \alpha \right)\tan \left( \beta \right)} \\
\end{align}$
Hence, the distance between the two depressions A and B from the tower is $BA=\dfrac{h\left( \tan \left( \beta \right)-\tan \left( \alpha \right) \right)}{\tan \left( \alpha \right)\tan \left( \beta \right)}$.

Note: We could have also equated the value of h from equation (i). But this would have converted the simple solution into a complex one. In case we need to find out the value of the distance in terms of $\cot \left( \theta \right)$ then, we would have used the substitution $\tan \left( \theta \right)=\dfrac{1}{\cot \left( \theta \right)}$ in the answer and get the required new answer. But this is only when it is asked in the question.