Question

From a right circular cylinder with height h and radius r, a right circular cone of the same height and the same base is removed. Find the volume of the remaining solid.

Answer 1

Hint: The volume of solid is the capacity that the solid has or can hold. It defines the volume of a liquid or any matter that it can hold. The shape of a cylinder is like a tube whereas the cone is an object that has a round base and a point at the top. We must know the formulae of the volumes of cylinder and cone in order to solve the given question.

Complete step-by-step answer:
The given question revolves around the concepts of mensuration. We are provided a right circular cylinder with height h and radius r. Out of this right circular cylinder, a right circular cone of the same base and the same height is removed.

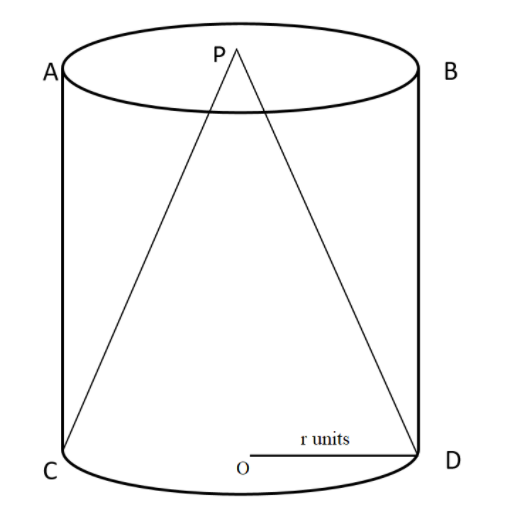
Now, we know that the formula for volume of a right circular cylinder is $ \pi {r^2}h $ , where r is the radius of the cylinder and h represents the height of a cylinder.
So, we get the volume of the cylinder with height h and radius r as $ \pi {r^2}h $ .
Also, we know that the formula for volume of a right circular cone is $ \dfrac{1}{3}\pi {r^2}h $ , where r is the radius of the cylinder and h represents the height of a cylinder.
So, we get the volume of the cone with height h and radius r as $ \dfrac{1}{3}\pi {r^2}h $ .
Now, the right circular cone is removed from the right circular cylinder and we have to find the volume of the remaining solid.
So, we get,
Volume of remaining solid $ = \pi {r^2}h - \dfrac{1}{3}\pi {r^2}h $
 $ = \dfrac{2}{3}\pi {r^2}h $
Hence, we get the volume of the remaining solid as $ \dfrac{2}{3}\pi {r^2}h $ .
So, the correct answer is “ $ \dfrac{2}{3}\pi {r^2}h $ ”.

Note: If any three dimensional shape is removed from a solid structure, then the volume is reduced. We can get the remaining volume of the solid by subtracting the volume of the shape from the solid. One should take care while doing the calculations in order to be sure of the answer.