Question

From a balloon vertically above a straight road, the angles of depression of two cars on an instant are found to be ${45^0}$ and ${60^0}$. If the cars are 100 m apart, find the height of the balloon.

Answer 1

Hint: Draw a proper diagram representing the information given in the question clearly. Then by observing the diagram, decide which trigonometric ratios to be used to calculate the height of the balloon. Angle of depression is equal to the angle of elevation.

Complete step-by-step answer:
Observe the diagram

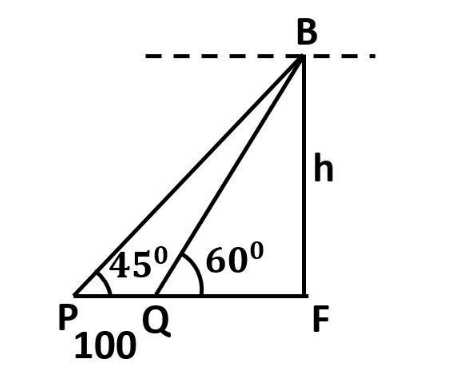
In the diagram above,
Let the balloon is at position B at a height $h$
P and Q are the respective positions of cars at a distance of 100 m apart from each other.
The balloon is making an angle of depression of ${45^0}$ with car P and of ${60^0}$ with car Q.
Then by using the triangular properties of trigonometric ratios. We can write
In $\Delta BQF$
$\tan {60^0} = \dfrac{{BF}}{{QF}}$
$ \Rightarrow \sqrt 3 = \dfrac{h}{{QF}}$ $\left( {\because \tan {{60}^0} = \sqrt 3 } \right)$
Rearranging it we can write
$QF = \dfrac{h}{{\sqrt 3 }}$
Now, in $\Delta BPF$
$\tan {45^0} = \dfrac{h}{{PF}}$
But $PF = PQ + QF$
$ \Rightarrow 1 = \dfrac{h}{{100 + \dfrac{h}{{\sqrt 3 }}}}$ $\left( {\because \tan {{45}^0} = 1,PQ = 100,QF = \dfrac{h}{{\sqrt 3 }}} \right)$
By simplifying it, we can write
$1 = \dfrac{h}{{\dfrac{{100\sqrt 3 + h}}{{\sqrt 3 }}}}$
$ \Rightarrow 1 = \dfrac{{h\sqrt 3 }}{{100\sqrt 3 + h}}$ $\left( {\because \dfrac{1}{{\dfrac{1}{x}}} = x} \right)$
By cross multiplying, we get
$100\sqrt 3 + h = h\sqrt 3 $
Rearranging it we can write
$h\sqrt 3 - h = 100\sqrt 3 $
By taking common terms out, we get
$(\sqrt 3 - 1)h = 100\sqrt 3 $
By dividing both the sides by $(\sqrt 3 - 1)$ we get
$h = \dfrac{{100\sqrt 3 }}{{\sqrt 3 - 1}}$
Therefore, the height of the balloon from the road is $\dfrac{{100\sqrt 3 }}{{\sqrt 3 - 1}}$
So, the correct answer is “$\dfrac{{100\sqrt 3 }}{{\sqrt 3 - 1}}$”.

Note: In this question, the angle of depression is given. But we used it as an angle of elevation. It does not make us wrong as angle of elevation and angle of depression is always the same. You can verify it using the property of interior angles of two parallel lines. Depicting which trigonometric ratio to use is the key point in this question. We used $\tan \theta $ because the base was given and we needed to find perpendicular.