Question

Form the differential equation of the family of circles in the second quadrant and touching coordinate axes.

Answer 1

Hint: We need to draw a diagram to visualize the circles which touches both $x\text{ and }y$ axes in the second quadrant and design the equation for the family of circles. We then differentiate with respect to $x$ and determine the value of any radius of the circles touching both axes in the second quadrant in terms of differentials and variables. Then we replace the value of radius to form the differential equation.

Complete step by step answer:
Let us draw any circle C from the family circles which touches both $x\text{ and }y$ axes in the second quadrant. We denote the radius of such a circle as $a$. The centre of the circle will be at a distance $a$ from both $x\text{ and }y$ axes. So the centre of the circle is given the coordinates$\left( -a,a \right)$. The circle is shown in the following figure.\[\]

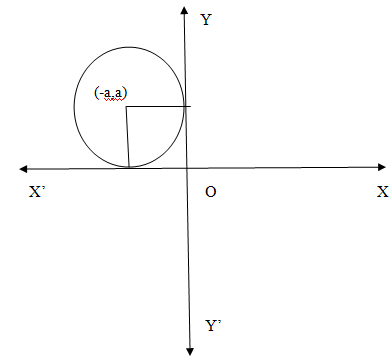
We know from the equation of the circle that the circle with origin at the centre and radius $r$ is given by the equation ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$.
So all such circles whose radius is $a$ and centred at $\left( -a,a \right)$ will be defined by the equation
\[\begin{align}
  & {{\left( x+a \right)}^{2}}+{{\left( y-a \right)}^{2}}={{a}^{2}}......(1) \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}-2ax+2ax+{{a}^{2}}=0 \\
\end{align}\]
Differentiating above equation with respect to $x$,
\[\begin{align}
  & 2x+2y\dfrac{dy}{dx}+2a-2a\dfrac{dy}{dx}=0 \\
 & \Rightarrow x+y\dfrac{dy}{dx}=a\dfrac{dy}{dx}-a \\
\end{align}\]
Substituting $\dfrac{dy}{dx}=y'$
\[\begin{align}
  & x+y{{y}^{'}}=ay{{y}^{'}}-a=a\left( y'-1 \right) \\
 & \Rightarrow a=\dfrac{x+y{{y}^{'}}}{y'-1}......(2) \\
\end{align}\]
Now we have obtained the value of $a$ we replace it in (1)
$ {\left({x + \dfrac{x+yy’}{y’-1}} \right)}^2 + {\left({y - \dfrac{x+yy’}{y’-1}} \right)} = {\left(\dfrac{x+yy’}{y’-1} \right)}^2$
\[
   \Rightarrow {\left( {x{y'} - x + x + y{y'}} \right)^2} + {\left( {y{y'} - y - x - y{y'}} \right)^2} = {\left( {x + y{y'}} \right)^2} \\
   \Rightarrow {\left( {x{y'} + y{y'}} \right)^2} + {\left( {x + y} \right)^2} = {\left( {x + y{y'}} \right)^2} \\
   \Rightarrow {\left( {x + y} \right)^2}{\left( {{y'} + 1} \right)^2} = {\left( {x + y{y'}} \right)^2} \\
\]
The above equation is the required differential equation.\[\]

Note: The questions test your knowledge of differential equations for a family of curves. We need to be careful during simplification as after squaring as calculation may become cumbersome in different routes. Similarly we can find out the differential equation for a family of parabola, ellipses, hyperbolas subjected to particular conditions.