Question

Form the differential equation of the family of ellipse having foci on the y-axis and centre at origin.

Answer 1

Hint: For solving this problem, we first try to form the general equation of ellipse passing through the origin having major axis at y and minor axis at x so that the foci lies on y-axis. After writing the general equation, we have to remove the variables a and b. To do so, we differentiate the whole equation until we obtain a variable free derivative form. This gives us the family of ellipses.

Complete step-by-step answer:
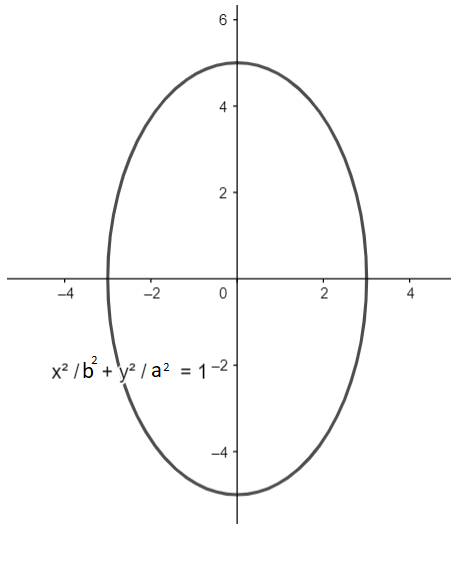
The general equation of ellipse passing through the origin having major axis at y and minor axis at x so that the foci lies on y axis can be given as: $\dfrac{{{x}^{2}}}{{{b}^{2}}}+\dfrac{{{y}^{2}}}{{{a}^{2}}}=1$, where a and b are major and minor axes respectively.

Some of the important differential rules which are useful can be stated as:
$\begin{align}
  & \dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}} \\
 & \dfrac{dy}{dx}={y}' \\
 & \dfrac{d}{dx}\left( mn \right)={m}'n+{n}'m \\
 & \dfrac{d}{dx}\left( \text{constant} \right)=0 \\
\end{align}$
Now, the above equation cannot represent the family of ellipses as it contains two variables. So, to eliminate these variables we use differentiation. Since there are two variables, we can easily differentiate the equation twice.
$\begin{align}
  & {{\left( \dfrac{{{x}^{2}}}{{{b}^{2}}}+\dfrac{{{y}^{2}}}{{{a}^{2}}} \right)}^{\prime }}={{\left( 1 \right)}^{\prime }} \\
 & \Rightarrow \dfrac{2x}{{{b}^{2}}}+\dfrac{2y{y}'}{{{a}^{2}}}=0 \\
 & \Rightarrow \dfrac{x}{{{b}^{2}}}+\dfrac{y{y}'}{{{a}^{2}}}=0 ………….(1)\\
\end{align}$
Again, differentiating with respect to x, we get
$\begin{align}
  & \Rightarrow {{\left( \dfrac{x}{{{b}^{2}}}+\dfrac{y{y}'}{{{a}^{2}}} \right)}^{\prime }}=0 \\
 & \Rightarrow {{\left( \dfrac{x}{{{b}^{2}}} \right)}^{\prime }}+{{\left( \dfrac{y{y}'}{{{a}^{2}}} \right)}^{\prime }}=0 \\
 & \Rightarrow \dfrac{1}{{{b}^{2}}}+\dfrac{y\cdot {y}''+{y}'\cdot {y}'}{{{a}^{2}}}=0 \\
 & \Rightarrow \dfrac{1}{{{b}^{2}}}=-\dfrac{y\cdot {y}''+{y}'\cdot {y}'}{{{a}^{2}}}\ldots \left( 2 \right) \\
\end{align}$
Substituting the value of equation (2) in the equation (1), we get
\[\begin{align}
  & \Rightarrow x\left[ -\dfrac{y\cdot {y}''+{y}'\cdot {y}'}{{{a}^{2}}} \right]+\dfrac{y\cdot {y}'}{{{a}^{2}}}=0 \\
 & \Rightarrow \dfrac{-x\cdot y\cdot {y}''-x\cdot {{\left( {{y}'} \right)}^{2}}+y\cdot {y}'}{{{a}^{2}}}=0 \\
 & \Rightarrow -x\cdot y\cdot {y}''-x\cdot {{\left( {{y}'} \right)}^{2}}+y\cdot {y}'=0 \\
 & \Rightarrow x\cdot y\cdot {y}''+x\cdot {{\left( {{y}'} \right)}^{2}}-y\cdot {y}'=0 \\
\end{align}\]
Hence, the family of ellipse is \[x\cdot y\cdot {y}''+x\cdot {{\left( {{y}'} \right)}^{2}}-y\cdot {y}'=0\].

Note: Knowledge of the family of equations is required for solving this problem. The family of equations should be free of arbitrary variables. Students must remember the key step of differentiation and the number of times they are allowed to do the differentiation.