Question

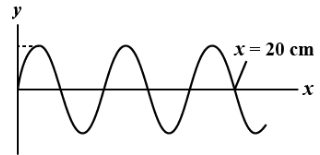
For the wave shown in figure, the frequency and wavelength, if its speed is $320\,m/s$ are

Answer 1

Hint: A wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities in physics, mathematics, and related fields, often represented by a wave equation. At least two field concentrations in the wave medium are present in physical waves. Periodic waves occur as quantities oscillate continuously around an equilibrium (resting) value at a certain frequency.

Complete answer:
The number of times a repeated event occurs per unit of time is known as frequency. It's also known as temporal frequency, which highlights the difference between spatial and angular frequency. The unit of frequency is hertz (Hz), which equals one occurrence per second. In mechanics, frequency refers to the number of waves that travel through a fixed point in a given amount of time, as well as the number of loops or movements that a body in periodic motion goes through in a given amount of time.

The number of waves that reach a fixed point in a given amount of time is known as wave frequency. The hertz (Hz) is the SI unit for wave frequency, with 1 hertz equalling 1 wave passing a fixed point in 1 second.The interval between two consecutive crests or troughs of a wave is known as its wavelength. It is calculated in the wave's direction. Frequency is inversely proportional to wavelength. This implies that the smaller the frequency, the longer the wavelength. From the given diagram, we deduce
$2.5\lambda = 20$
$\Rightarrow \lambda = \dfrac{{20}}{{2.5}} = 8\;{\text{cm}}$
Hence, $\lambda = 8\;{\text{cm}}$
We know that
$\nu = \dfrac{v}{\lambda }$
\[\Rightarrow v = 320\]
$\Rightarrow \lambda = 8\;{\text{cm = 8 x 1}}{{\text{0}}^{ - 2}}\,m$
Substitute the values in the formula to get,
$\nu = \dfrac{{320}}{{8 \times {{10}^{ - 2}}}} \\
\therefore \nu= 4000\,Hz$
Frequency = 4000 Hz

Hence, the frequency and wavelength are 4000 Hz and $8 \times 1{{\text{0}}^{ - 2}}\,m$.

Note: The wavelength of a periodic wave is its spatial time, or the distance over which the wave's form repeats. It's the difference between two adjacent corresponding points of the same phase on the wave, including two neighbouring crests, troughs, or zero crossings, and it's a feature of both moving and stationary waves, as well as other spatial wave patterns. The spatial frequency is the opposite of the wavelength. Modulated waves, as well as the sinusoidal envelopes of modulated waves or waves produced by the interference of multiple sinusoids, are often referred to as wavelengths.