Question

How do you find the vertex and the intercepts for $f\left( x \right) = 2{x^2} - 12x + 21$?

Answer 1

Hint: We have to find the vertex and the intercepts for $f\left( x \right) = 2{x^2} - 12x + 21$. First rewrite the equation in vertex form. Next, use the vertex form of parabola, to determine the values of $a$, $h$, and $k$. Next, find the vertex by putting the value of $h$ and . Then, find the $y$-intercept by substituting $0$ for $x$ in $f\left( x \right) = 2{x^2} - 12x + 21$. Then, find the $x$-intercept by substituting $0$ for $y$ in vertex form of equation.
Vertex form of a parabola: $a{\left( {x + d} \right)^2} + e$
$d = \dfrac{b}{{2a}}$
$e = c - \dfrac{{{b^2}}}{{4a}}$
Vertex form: $y = a{\left( {x - h} \right)^2} + k$
Vertex: $\left( {h,k} \right)$
$p = \dfrac{1}{{4a}}$
Focus: $\left( {h,k + p} \right)$
Directrix: $y = k - p$

Complete step by step answer:
We have to find the vertex and the intercepts for $f\left( x \right) = 2{x^2} - 12x + 21$.
So, compare $2{x^2} - 12x + 21$ with $a{x^2} + bx + c$.
So, first rewrite the equation in vertex form.
For this, complete the square for $2{x^2} - 12x + 21$.
Use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$.
$a = 2,b = - 12,c = 21$
Consider the vertex form of a parabola.
$a{\left( {x + d} \right)^2} + e$
Now, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$.
$d = \dfrac{{ - 12}}{{2 \times 2}}$
Simplify the right side.
$ \Rightarrow d = - 3$
Find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$.
$e = 21 - \dfrac{{{{\left( { - 12} \right)}^2}}}{{4 \times 2}}$
$ \Rightarrow e = 3$
Now, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$.
$2{\left( {x - 3} \right)^2} + 3$
Set $y$ equal to the new right side.
$y = 2{\left( {x - 3} \right)^2} + 3$
Now, use the vertex form, $y = a{\left( {x - h} \right)^2} + k$, to determine the values of $a$, $h$, and $k$.
$a = 2$
$h = 3$
$k = 3$
Since the value of $a$ is positive, the parabola opens up.
Opens Up
Find the vertex $\left( {h,k} \right)$.
$\left( {3,3} \right)$
Find the $y$-intercept.
Use the original equation, and substitute $0$ for $x$.
$f\left( 0 \right) = 2{\left( 0 \right)^2} - 12\left( 0 \right) + 21$
$ \Rightarrow f\left( 0 \right) = 21$
Therefore, the $y$-intercept is $\left( {0,21} \right)$.
Find the $x$-intercept.
Use equation $y = 2{\left( {x - 3} \right)^2} + 3$, and substitute $0$ for $y$.
$2{\left( {x - 3} \right)^2} = - 3$
$ \Rightarrow {\left( {x - 3} \right)^2} = - \dfrac{3}{2}$
$ \Rightarrow x - 3 = \pm \sqrt {\dfrac{3}{2}} i$
$ \Rightarrow x = 3 + \sqrt {\dfrac{3}{2}} i,3 - \sqrt {\dfrac{3}{2}} i$
Since, $x$ is a complex number. Thus, $f\left( x \right)$ has no $x$-intercepts.
Hence, for $f\left( x \right) = 2{x^2} - 12x + 21$
Vertex: $\left( {3,3} \right)$
$y$-intercept: $\left( {0,21} \right)$
$x$-intercept: No intercepts

Note: We can also determine the vertex and the intercepts for $f\left( x \right) = 2{x^2} - 12x + 21$ by plotting it.
Graph of $f\left( x \right) = 2{x^2} - 12x + 21$:

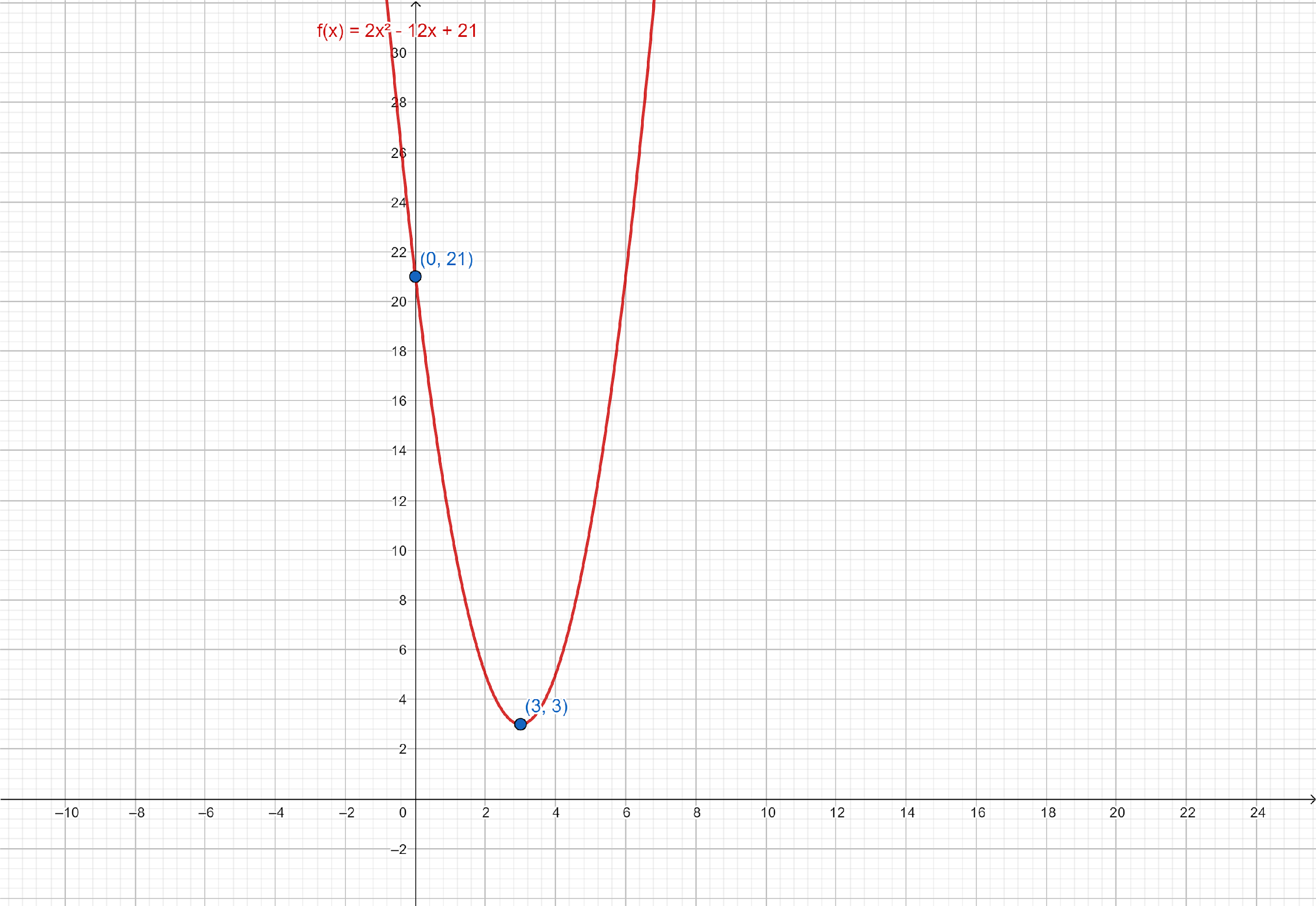
Hence, for $f\left( x \right) = 2{x^2} - 12x + 21$
Vertex: $\left( {3,3} \right)$
$y$-intercept: $\left( {0,21} \right)$
$x$-intercept: No intercepts