Question

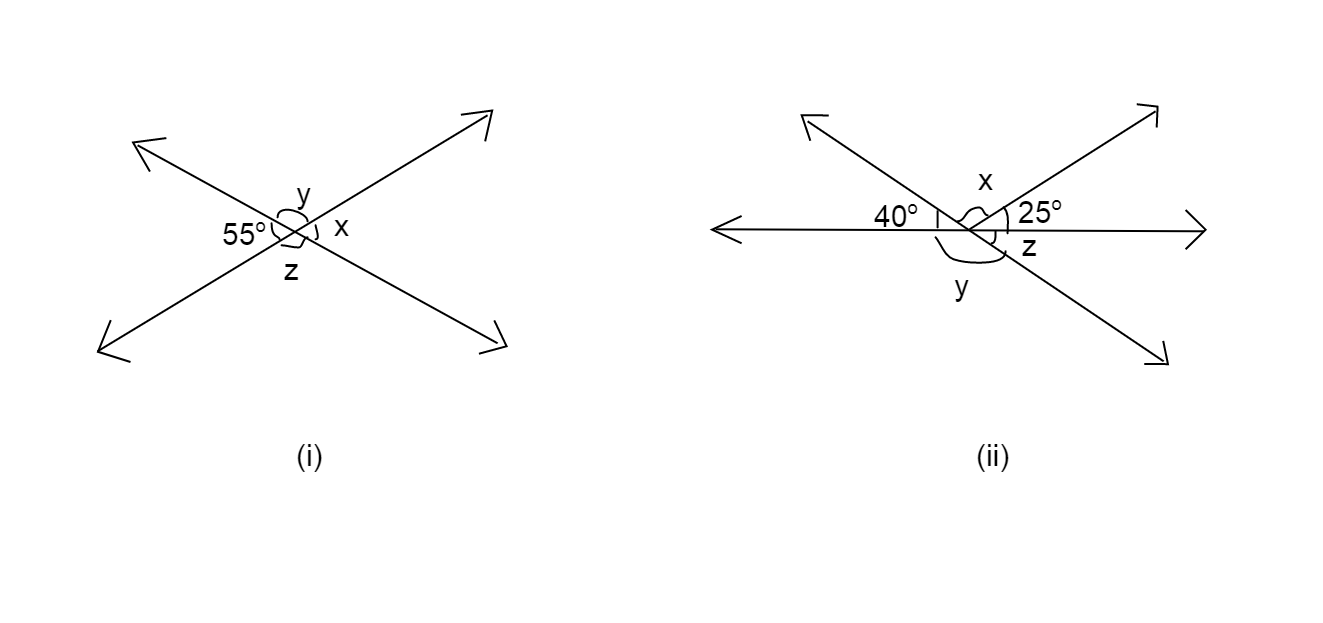
Find the values of the angles $x,y$ and $z$ in each of the following:

Answer 1

Hint: To find the unknown angles we can use the fact that they are opposite to known angles and opposite angles are equal. Also the sum of angles across a line is equal to $180^\circ $. Using these facts, we can find the unknown angles.

Useful formula:
When two lines intersect, we have two results.
(i) opposite angles formed are equal.
(ii) angle sum in a line is ${180^ \circ }$.
The latter holds for more than two lines as well.

Complete step by step solution:
Consider figure (i).
When two lines intersect, opposite angles formed are equal.
Using this result we have, $x = 55^\circ $ and $y = z$
And also angle sum in a line is ${180^ \circ }$.
This gives $y + 55^\circ = 180^\circ $
Simplifying we have,
$ \Rightarrow y = 180^\circ - 55^\circ = 125^\circ $
$ \Rightarrow y = 125^\circ $
And $y = z \Rightarrow z = 125^\circ $
$\therefore x = 55^\circ ,y = 125^\circ ,z = 125^\circ $

Now consider figure (ii).
Angle sum in a line is ${180^ \circ }$.
$ \Rightarrow 40^\circ + x + 25^\circ = 180^\circ $
Simplifying we get,
$x + 65^\circ = 180^\circ $
$ \Rightarrow x = 180^\circ - 65^\circ = 115^\circ $
$ \Rightarrow x = 115^\circ $
Also, $40^\circ + y = 180^\circ $
Simplifying we get,
$ \Rightarrow y = 180^\circ - 40^\circ = 140^\circ $
Also $y + z = {180^ \circ }$
Substituting for $y$ we get,
$ \Rightarrow {140^ \circ } + z = {180^ \circ }$
Simplifying we get,
$ \Rightarrow z = {180^ \circ } - {140^ \circ } = {40^ \circ }$
$ \Rightarrow z = {40^ \circ }$
$\therefore $ We have, $x = 115^\circ ,y = 140^\circ ,z = 40^\circ $

Additional information:
The sum of angles around a point is $360^\circ $.
If two angles are said to be complementary, then the sum of the two angles is $180^\circ $.
Also, two angles are complementary means, the sum of the two angles is ${90^ \circ }$.

Note:There are other methods to solve this question. In the first figure, we can take $55^\circ $ and $z$ as supplementary angles instead of what we have taken. Also, in the second figure we can consider $40^\circ $ and $x$ as opposite angles. In either way we can get to the answer.