Question

Find the value of trigonometric expression $\tan 315{}^\circ $ .

Answer 1

Hint:Write the angle inside the trigonometric function given in problem to acute trigonometric relation. i.e. between ${{0}^{\circ }}$ to ${{90}^{\circ }}$ (or $\dfrac{\pi }{2}$ ). And use the quadrant rules that tan function is positive in the first and third quadrant and negative in the second and fourth quadrant. If the angle in tan function has involvement of multiple of $\dfrac{\pi }{2}$ (not $\pi $) i.e. of type $\dfrac{n\pi }{2}\pm \theta $ , then change tan function to cot or if summation of angle is of type $n\pi \pm \theta $ , then do not change the trigonometric function. Use the above rules to get the answer. Use $:\tan \left( \dfrac{\pi }{6} \right)=\dfrac{1}{\sqrt{3}}$ .

Complete step-by-step answer:
The given expression in the problem is $=\tan 315{}^\circ $ .
Let us suppose the value of the given expression is ‘M’, So, we can write equation as –
\[M=\tan 315{}^\circ \] ……………………………….. (i)
Now, we can observe that the angle involved in the above expression is not lying in $0{}^\circ $ to ${{90}^{\circ }}$. It means we have to convert the given angle to acute angle form with the help of some trigonometric identities.
Hence, Let us divide the given expression by ${{180}^{\circ }}$ . So, that we can write the given angle in form of sum of angle which is multiple of ${{180}^{\circ }}$in following way:-
$315=180\times 2-45$ ……………………………………….. (ii)
Now, as we know the radian representation of $180{}^\circ $ is given as –
$\pi $radian $=180{}^\circ $ ………………… (iii)
And with the help of above relation, we can re-write the angle ${{45}^{\circ }}$ in radian form as well, given as –
${{45}^{\circ }}=\dfrac{\pi }{4}radian$ …………… (iv)
Hence, we can write the equation (ii) as –
$315=2\pi -\dfrac{\pi }{4}$ ……………………………………. (iii)
Now, we can re-write the given expression in the problem i.e. equation (i) as –
$M=\tan \left( 2\pi -\dfrac{\pi }{4} \right)$ ……………………………. (iv)
Now, as we know the quadrant angles are defined as

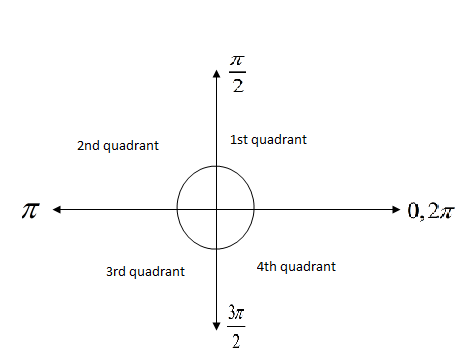
Now, we can apply the trigonometric rules for conversion of trigonometric expressions by changing its angle. We can observe the angle in equation (iv) and hence get that the angle \[\left( 2\pi -\dfrac{\pi }{4} \right)\] will lie definitely in 4th quadrant as \[2\pi \] will lie at same position where 0 lying (after first rotation to ${{360}^{\circ }}$ or \[2\pi \]).
So, we know that tan function is negative in the 4th quadrant and we know very well that the angle involved in the equation (iv) is \[2\pi \] i.e. multiple of $\pi $ . So, the trigonometric function will not change while changing the angle as per the trigonometric rules for conversion.
So, we can write trigonometric identity as –
$\tan \left( 2\pi -\theta \right)=-\tan \theta $ ……………….. (v)
Hence, using the equation (v), we can get the equation (iv) as –
$\begin{align}
  & M=\tan \left( 2\pi -\dfrac{\pi }{4} \right)=-\tan \dfrac{\pi }{4} \\
 & M=-\tan \dfrac{\pi }{4} \\
\end{align}$
Now, we know the value of tan$\dfrac{\pi }{4}$ or $\tan 45{}^\circ $ is given as 1. So, we get the value of M as –
M=-1
Hence, the value of the given expression in the problem is -1. So, we get –
$\tan 315{}^\circ =-1$ .
So, ‘$-1$’ is the answer to the problem.

Note: Don’t go for calculating the exact value directly with any other identity, it will be a complex approach and may give wrong answers as well. So, always try to solve these kinds of questions by the way given in solution.One can apply the trigonometric identity with the negative expression directly without changing the angles in radian form. It is done in the solution because we are more familiar with the trigonometric relation given in solution in radian form only.So, don’t confuse with that part of the solution, you can evaluate the given expression by using degree form of angle as well.