Question

Find the value of tetrahedron V – ABC if V is (1, 1, 1), A is (1, 2, 3), B is (2, 3, 4) and C is (2, 3, - 1).

Answer 1

Hint: We will be using the basic concept of vectors and 3-D geometry to solve the problem. We will be using a scalar triple product of vectors to solve the problem.

Complete step by step answer:
We can draw the tetrahedron V – ABC as below,

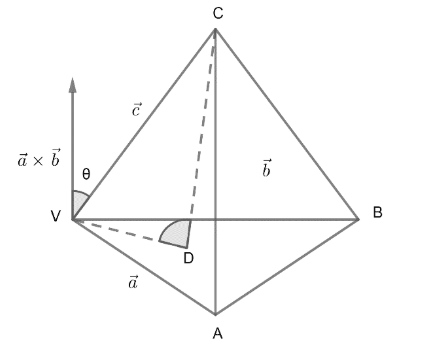
Here,
$\begin{align}
  & \overset{\to }{\mathop{VA}}\,=\overset{\to }{\mathop{a}}\, \\
 & \overset{\to }{\mathop{VB}}\,=\overset{\to }{\mathop{b}}\, \\
 & \overset{\to }{\mathop{VC}}\,=\overset{\to }{\mathop{c}}\, \\
\end{align}$
Now, we have to find the volume of the tetrahedron. For this we know that,
The volume of tetrahedron $=\dfrac{1}{3}\left( base\times height \right).......\left( 1 \right)$
Now, we have to find the base of the tetrahedron. Considering $\Delta VAB$ as base. The base area can be written as $base=\dfrac{1}{2}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right|$
Now, we have to find the height of the tetrahedron considering $\Delta VAB$ as base.
By taking $\Delta OAB$ as base. We can write height as $\left| \overset{\to }{\mathop{c}}\, \right|\cos \theta $, where $\theta $ is the angle between $\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right)\ and\ \overset{\to }{\mathop{c}}\,$.
So,
The volume of tetrahedron $=\dfrac{1}{3}\left( base\ area\times height \right)$
\[\begin{align}
  & =\dfrac{1}{3}\left( \dfrac{1}{2}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right| \right)\left( \left| \overset{\to }{\mathop{c}}\, \right|\cos \theta \right) \\
 & =\dfrac{1}{6}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right|\left| \overset{\to }{\mathop{c}}\, \right|\cos \theta \\
 & \text{Using }\overset{\to }{\mathop{A}}\,.\overset{\to }{\mathop{B}}\,=\overset{\to }{\mathop{A}}\,\overset{\to }{\mathop{B}}\,\cos \theta \\
 & =\dfrac{1}{6}\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right) \\
\end{align}\]
Now, we know that,
$\begin{align}
  & \overset{\to }{\mathop{VA}}\,=\overset{\to }{\mathop{a}}\,=\left( 1-1 \right)\overset{\hat{\ }}{\mathop{i}}\,+\left( 2-1 \right)\overset{\hat{\ }}{\mathop{j}}\,+\left( 3-1 \right)\overset{\hat{\ }}{\mathop{k}}\, \\
 & \overset{\to }{\mathop{VB}}\,=\overset{\to }{\mathop{b}}\,=\left( 2-1 \right)\overset{\hat{\ }}{\mathop{i}}\,+\left( 3-1 \right)\overset{\hat{\ }}{\mathop{j}}\,+\left( 4-1 \right)\overset{\hat{\ }}{\mathop{k}}\, \\
 & \overset{\to }{\mathop{VC}}\,=\overset{\to }{\mathop{c}}\,=\left( 2-1 \right)\overset{\hat{\ }}{\mathop{i}}\,+\left( 3-1 \right)\overset{\hat{\ }}{\mathop{j}}\,+\left( -1-1 \right)\overset{\hat{\ }}{\mathop{k}}\, \\
\end{align}$
Now, we that the vector triple product of three vectors,
$\begin{align}
  & \overset{\to }{\mathop{a}}\,={{x}_{1}}\overset{\hat{\ }}{\mathop{i}}\,+{{y}_{1}}\overset{\hat{\ }}{\mathop{j}}\,+{{z}_{1}}\overset{\hat{\ }}{\mathop{k}}\, \\
 & \overset{\to }{\mathop{b}}\,={{x}_{2}}\overset{\hat{\ }}{\mathop{i}}\,+{{y}_{2}}\overset{\hat{\ }}{\mathop{j}}\,+{{z}_{2}}\overset{\hat{\ }}{\mathop{k}}\, \\
 & \overset{\to }{\mathop{c}}\,={{x}_{3}}\overset{\hat{\ }}{\mathop{i}}\,+{{y}_{3}}\overset{\hat{\ }}{\mathop{j}}\,+{{z}_{3}}\overset{\hat{\ }}{\mathop{k}}\, \\
\end{align}$
It can be solved as a matrix. For example,
\[\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right)=\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & {{z}_{1}} \\
   {{x}_{2}} & {{y}_{2}} & {{z}_{2}} \\
   {{x}_{3}} & {{y}_{3}} & {{z}_{3}} \\
\end{matrix} \right|\]
So, using this we can find the volume of tetrahedron as,
\[\dfrac{1}{6}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right|=\dfrac{1}{6}\left| \begin{matrix}
   0 & 1 & 2 \\
   1 & 2 & 3 \\
   1 & 2 & -2 \\
\end{matrix} \right|\]
Now, we can expand the matrix along R as,
$\begin{align}
  & 0\left( -4-6 \right)-1\left( -2-3 \right)+2\left( 2-2 \right) \\
 & -10-1\left( -5 \right)+2\left( 0 \right) \\
 & -10+5 \\
 & -5 \\
\end{align}$
So, the volume of tetrahedron is,
$\begin{align}
  & =\dfrac{1}{6}\left| -5 \right| \\
 & =\dfrac{5}{6} \\
\end{align}$
Hence, $\dfrac{5}{6}$ is the volume of the given tetrahedron.

Note: The question is calculation intensive. It is advised to do the calculation carefully also remembering some formula like that of finding volume of tetrahedron simplifies the problem to a great extent.
Volume of tetrahedron \[=\dfrac{1}{2}\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right)\]