Question

Find the value of \[\sin x,\cos x\,,\sec x\] if \[\tan x=\dfrac{-5}{12}\] lies in the second quadrant

Answer 1

Hint: The quadrants mentioned here are the quadrants we see in the graphs.
The sign of a trigonometric function is dependent on the signs of the coordinates of the points on the terminal side of the angle. all values other than \[\sin x\,\,\,\,\text{and }\operatorname{cosec}x\]are negative in the 2nd quadrant. all values other than \[\cos x\text{ and }\sec x\] are negative in the 4th quadrant. All values other than \[\tan x\,\,\text{ and }\cot x\] are negative in the 3rd quadrant. And all values of \[\sin x\,\,,\text{ }\operatorname{cosec}x\,,\,\,\,\,\tan x\,\,,\text{ }\cot x\,,\,\,\cos x\text{ and }\sec x\] is positive in 1st quadrant.
Since we have perpendicular and base values of the triangle through \[\tan x=\dfrac{-5}{12}\].
we will use the Pythagoras rule to find the values of those other trigonometric functions.

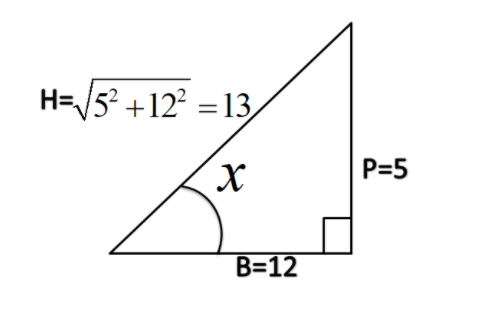
Complete step by step solution:
 \[\tan x\]is perpendicularly divided by the base of a triangle with a given value of angle \[x\], we can say that perpendicular P=5 and base B=12.
Thus by hypotenuse rule \[h=\sqrt{{{p}^{2}}+{{b}^{2}}}=\sqrt{{{5}^{2}}+{{12}^{2}}}=\sqrt{169}=13\] we get hypotenuse H=13.
In the second quadrant only the value of \[\sin x\,\,\,\,\text{and }\operatorname{cosec}x\] can be positive.
Therefore, the value of \[\sin x,\cos x\,,\sec x\] will be,
\[\begin{align}
  & \sin x=\dfrac{\text{P}}{\text{H}}=\dfrac{5}{13} \\
 & \cos x=\dfrac{\text{B}}{\text{H}}=-\dfrac{12}{13}\,\,\,\text{ } \\
 & \sec x=\dfrac{1}{\cos x}=\dfrac{-13}{12} \\
\end{align}\][since it lies in the second quadrant]
Since \[\sin x\]is perpendicularly divided by hypotenuse, \[\cos x\]is base divided by hypotenuse and \[\sec x\]is 1 divided by \[\cos x\].
Therefore the answer is \[\sin x=\dfrac{5}{13}\,\,\,,\cos x=-\dfrac{12}{13},\,\,\,\text{ }\sec x=\dfrac{-13}{12}\].


Additional information: The distance from a point to the origin is always positive, but the signs of the x and y coordinates may be positive or negative. Thus, in the first quadrant, where x and y coordinates are all positive, all six trigonometric functions have positive values. In the second quadrant, only sine and cosecant (the reciprocal of sine) are positive. In the third quadrant, only tangent and cotangent are positive. Finally, in the fourth quadrant, only cosine and secant are positive.


Note: the values of \[\sin x,\cos x\,,\sec x\] can be easily found out by using, \[\sin x\] is perpendicular divided by hypotenuse, \[\cos x\]is base divided by hypotenuse and \[\sec x\] is 1 divided by \[\cos x\]. To complete this question we should have a proper idea of what quadrants are and how it changes the values for other trigonometric functions.
A rough sketch of a right-angled triangle through the values of perpendicular, base, and hypotenuse found by us will also help us further.