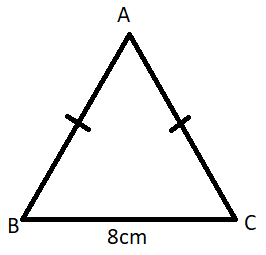
Find the value of ${{\sin }^{2}}B+{{\cos }^{2}}B$:
Answer
Verified359.1k+ views
Hint: First observe that the given triangle is an isosceles triangle because its two sides: AB and AC are given equal. Draw a perpendicular AD from A to BC. Use the property that if a perpendicular is drawn from the common vertex of the equal sides, then the perpendicular bisects the third side into two equal parts. Then apply the Pythagoras theorem on $\Delta $ ABD.
Complete step-by-step answer:
In this question, we need to find the value of ${{\sin }^{2}}B+{{\cos }^{2}}B$ .
We can see in the diagram that the given triangle is an isosceles triangle because its two sides: AB and AC are given equal.
To solve this question, we will draw a perpendicular AD from A to BC.
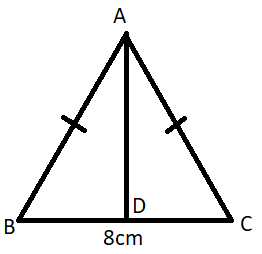
We know the property of an isosceles triangle that if a perpendicular is drawn from the common vertex of the equal sides, then the perpendicular bisects the third side into two equal parts.
Using this property, we come to know that
BD = DC = 4 cm.
Now we will apply the Pythagoras theorem on $\Delta $ ABD.
First let us define the Pythagoras theorem.
The Pythagoras theorem states that: In a right-angled triangle, the square of hypotenuse is equal to the sum of the squares of its other two sides.
Now, since $\Delta $ ABD is a right-angled triangle, we will apply the Pythagoras theorem on it.
Using this property, we come to know that:
$A{{D}^{2}}+B{{D}^{2}}=A{{B}^{2}}$
We know that BD = 4 cm
Let AB = x cm.
Now applying the Pythagoras theorem, we get:
$\Rightarrow$ $A{{D}^{2}}+{{4}^{2}}={{x}^{2}}$
$\Rightarrow$ $A{{D}^{2}}={{x}^{2}}-16$
$\Rightarrow$ $AD=\sqrt{{{x}^{2}}-16}$ …(1)
Now, we will find the values of ${{\sin }^{2}}B$ and ${{\cos }^{2}}B$ in terms of x.
$\Rightarrow$ $\sin B=\dfrac{AD}{AB}=\dfrac{\sqrt{{{x}^{2}}-16}}{x}$
So, ${{\sin }^{2}}B=\dfrac{{{x}^{2}}-16}{{{x}^{2}}}$
$\Rightarrow$ $\cos B=\dfrac{BD}{AB}=\dfrac{4}{x}$
So, ${{\cos }^{2}}B=\dfrac{16}{{{x}^{2}}}$
Now, we will add these to get the final answer:
$\Rightarrow$ ${{\sin }^{2}}B+{{\cos }^{2}}B=\dfrac{{{x}^{2}}-16}{{{x}^{2}}}+\dfrac{16}{{{x}^{2}}}$
$\Rightarrow$ ${{\sin }^{2}}B+{{\cos }^{2}}B=\dfrac{{{x}^{2}}-16+16}{{{x}^{2}}}$
$\Rightarrow$ ${{\sin }^{2}}B+{{\cos }^{2}}B=\dfrac{{{x}^{2}}}{{{x}^{2}}}=1$
Hence, ${{\sin }^{2}}B+{{\cos }^{2}}B=1$
This is our final answer.
Note: The value which we found in this question ${{\sin }^{2}}B+{{\cos }^{2}}B=1$ is a very popular and very important property in trigonometry which serves the base for many other theories. In the future, you can directly use this property for any angle as this is true for all angles.
Complete step-by-step answer:
In this question, we need to find the value of ${{\sin }^{2}}B+{{\cos }^{2}}B$ .
We can see in the diagram that the given triangle is an isosceles triangle because its two sides: AB and AC are given equal.
To solve this question, we will draw a perpendicular AD from A to BC.
We know the property of an isosceles triangle that if a perpendicular is drawn from the common vertex of the equal sides, then the perpendicular bisects the third side into two equal parts.
Using this property, we come to know that
BD = DC = 4 cm.
Now we will apply the Pythagoras theorem on $\Delta $ ABD.
First let us define the Pythagoras theorem.
The Pythagoras theorem states that: In a right-angled triangle, the square of hypotenuse is equal to the sum of the squares of its other two sides.
Now, since $\Delta $ ABD is a right-angled triangle, we will apply the Pythagoras theorem on it.
Using this property, we come to know that:
$A{{D}^{2}}+B{{D}^{2}}=A{{B}^{2}}$
We know that BD = 4 cm
Let AB = x cm.
Now applying the Pythagoras theorem, we get:
$\Rightarrow$ $A{{D}^{2}}+{{4}^{2}}={{x}^{2}}$
$\Rightarrow$ $A{{D}^{2}}={{x}^{2}}-16$
$\Rightarrow$ $AD=\sqrt{{{x}^{2}}-16}$ …(1)
Now, we will find the values of ${{\sin }^{2}}B$ and ${{\cos }^{2}}B$ in terms of x.
$\Rightarrow$ $\sin B=\dfrac{AD}{AB}=\dfrac{\sqrt{{{x}^{2}}-16}}{x}$
So, ${{\sin }^{2}}B=\dfrac{{{x}^{2}}-16}{{{x}^{2}}}$
$\Rightarrow$ $\cos B=\dfrac{BD}{AB}=\dfrac{4}{x}$
So, ${{\cos }^{2}}B=\dfrac{16}{{{x}^{2}}}$
Now, we will add these to get the final answer:
$\Rightarrow$ ${{\sin }^{2}}B+{{\cos }^{2}}B=\dfrac{{{x}^{2}}-16}{{{x}^{2}}}+\dfrac{16}{{{x}^{2}}}$
$\Rightarrow$ ${{\sin }^{2}}B+{{\cos }^{2}}B=\dfrac{{{x}^{2}}-16+16}{{{x}^{2}}}$
$\Rightarrow$ ${{\sin }^{2}}B+{{\cos }^{2}}B=\dfrac{{{x}^{2}}}{{{x}^{2}}}=1$
Hence, ${{\sin }^{2}}B+{{\cos }^{2}}B=1$
This is our final answer.
Note: The value which we found in this question ${{\sin }^{2}}B+{{\cos }^{2}}B=1$ is a very popular and very important property in trigonometry which serves the base for many other theories. In the future, you can directly use this property for any angle as this is true for all angles.
Last updated date: 21st Sep 2023
•
Total views: 359.1k
•
Views today: 8.59k
