Question

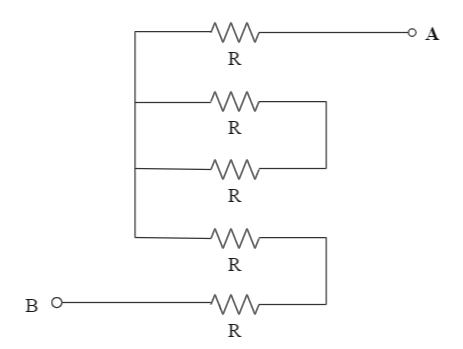
Find the value of $ {R_{AB}} $ in the given circuit.

A. $ 5R $
B. $ 3.5R $
C. $ \dfrac{{3R}}{2} $
D. $ 3R $

Answer 1

Hint
There are two types of common combinations of resistances: Series and Parallel. In Series combination, the resistances add up linearly, while in a Parallel sequence, he reciprocals of resistances add up.
$\Rightarrow {R_{eq}} = {R_1} + {R_2} $ for Series combination.
$\Rightarrow {R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} $ for Parallel combination.
$\Rightarrow {R_1} $ and $ {R_2} $ are the intermediate resistances.

Complete step by step answer
The given circuit is a combination of identical resistances joined in series and parallel alike. We start from point A towards point B to calculate the equivalent resistance.
As we start from point A, we encounter a resistance R, followed by two resistances connected in parallel. Moving forward, we see two more resistances connected in series with the last parallel combination.
We know that a series combination can be solved as:
$\Rightarrow {R_{eq}} = {R_1} + {R_2} $
So, if we write it all down:
Total resistance is given by $ {R_{AB}} = R + {\text{parallel}}(R{\text{ and }}R) + R + R $ [Eq. 1]
We calculate the total parallel resistance as:
$\Rightarrow {R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} $ where both $ {R_1} $ and $ {R_2} $ are equal to $ R $ . This gives us:
$\Rightarrow {R_p} = \dfrac{{R \times R}}{{R + R}} = \dfrac{{R \times R}}{{2R}} $
This gives us the parallel resistance as $ {R_p} = \dfrac{R}{2} $ .
Now combining all these together and putting in Eq. 1, we get:
$\Rightarrow {R_{AB}} = R + {R_p} + R + R $
$\Rightarrow {R_{AB}} = 3R + \dfrac{R}{2} = \dfrac{{6R + R}}{2} $ [Taking the LCM]
Finally, we get
$\Rightarrow {R_{AB}} = \dfrac{{7R}}{2} = 3.5R $
Hence, the correct answer is option (B).

Note
In case of complicated circuits like this, where we need to find the total resistance between two points, a good practice is to pretend as if you took both end points and stretched them out. This makes it easier to visualise the circuits. As you pretend to stretch the wire, the series combination resistances will fall in a straight line, and you will be clearly able to see the parallel sequence, too.