Question

Write the formula to find the shortest distance between two straight lines whose vector equations are $\vec{r}=\overrightarrow{{{a}_{1}}}+\lambda \overrightarrow{{{b}_{1}}}\text{ and }\vec{r}=\overrightarrow{{{a}_{2}}}+\pi \overrightarrow{{{b}_{2}}}$ where $\lambda \text{ and }\pi $ are scalars.

Answer 1

Hint: In this question, we are given an equation of two lines in vector notation and we have to find the shortest distance between them. For that, we will first observe the lines and then determine if the lines are parallel or skew lines. After that, we will state the formula for finding the shortest distance between lines according to, if lines are parallel or skew.

Complete step-by-step solution:
Here, we are given pair of lines in vector form as $\vec{r}=\overrightarrow{{{a}_{1}}}+\lambda \overrightarrow{{{b}_{1}}}\text{ and }\vec{r}=\overrightarrow{{{a}_{2}}}+\pi \overrightarrow{{{b}_{2}}}$ where $\lambda \text{ and }\pi $ are scalars.
As we can see, one line has $\overrightarrow{{{b}_{1}}}$ and another line has $\overrightarrow{{{b}_{2}}}$ therefore, they are not parallel. So, these lines are skew lines.
Skew lines are the lines in three-dimensional geometry that do not intersect and not parallel.
We need to find the shortest distance between these two skew lines. The shortest distance between a pair of skew lines can be found by obtaining the length of the line segment that melts perpendicularly with both lines.

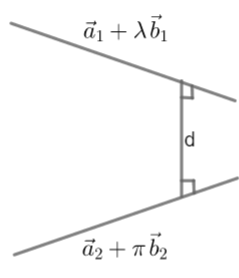
In this figure, length of d is the shortest distance. Formula for finding shortest distance between two skew lines $\vec{r}=\overrightarrow{{{a}_{1}}}+\lambda \overrightarrow{{{b}_{1}}}\text{ and }\vec{r}=\overrightarrow{{{a}_{2}}}+\pi \overrightarrow{{{b}_{2}}}$ where $\lambda \text{ and }\pi $ are scalars is given by
\[d=\left| \dfrac{\left( \overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}} \right)\cdot \left( \overrightarrow{{{a}_{2}}}-\overrightarrow{{{a}_{1}}} \right)}{\left| \overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}} \right|} \right|\]
Where $\overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}}$ represents cross product between $\overrightarrow{{{b}_{1}}}\text{ and }\overrightarrow{{{b}_{2}}}$ and can be given by $\overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}}=\left| \overrightarrow{{{b}_{1}}} \right|\left| \overrightarrow{{{b}_{2}}} \right|\sin \theta \hat{n}$ where $\left| \overrightarrow{{{b}_{1}}} \right|,\left| \overrightarrow{{{b}_{2}}} \right|$ represents magnitude of $\overrightarrow{{{b}_{1}}}\text{ and }\overrightarrow{{{b}_{2}}}$.
Hence, shortest distance between lines $\vec{r}=\overrightarrow{{{a}_{1}}}+\lambda \overrightarrow{{{b}_{1}}}\text{ and }\vec{r}=\overrightarrow{{{a}_{2}}}+\pi \overrightarrow{{{b}_{2}}}$ is equal to $\left| \dfrac{\left( \overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}} \right)\cdot \left( \overrightarrow{{{a}_{2}}}-\overrightarrow{{{a}_{1}}} \right)}{\left| \overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}} \right|} \right|$.

Note: Students should take care that, in the formula, if $\overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}}$ is taken then we have to take $\overrightarrow{{{a}_{2}}}-\overrightarrow{{{a}_{1}}}$ and if we take $\overrightarrow{{{b}_{2}}}\times \overrightarrow{{{b}_{1}}}$ then we have to take $\overrightarrow{{{a}_{1}}}-\overrightarrow{{{a}_{2}}}$. Students should note that $\overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}}\ne \overrightarrow{{{b}_{2}}}\times \overrightarrow{{{b}_{1}}}$. $\left| \overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}} \right|$ represents magnitude of $\overrightarrow{{{b}_{1}}}\times \overrightarrow{{{b}_{2}}}$. Students should not get confused that if lines are not parallel then they should be intersecting. We are talking about three dimensional geometry here, so there exist lines which are neither parallel nor do they intersect.