Question

How do you find the supplement of a radian measure?

Answer 1

Hint: Here we will use the total of all the angles of a triangle and then compare it to its radian measurement.
Also, we will use the concept of supplement. Finally we get the required answer

Formula used: In a triangle there are three angles that coincide the sides of a triangle and the sum of all the angles is \[ = {180^ \circ }\].
Let's say, following \[ABC\] is a triangle.

Then \[\angle ABC + \angle BCA + \angle BAC = {180^ \circ }\].
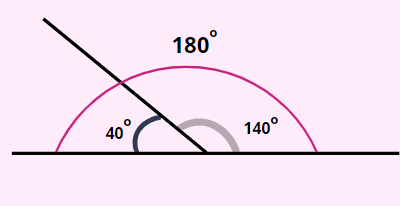
Two angles are called supplementary when summation of those two angles are equal to \[{180^ \circ }\].
Suppose one angle is measured as \[{140^ \circ }\], then its supplementary angle will be\[ = {180^ \circ } - {40^ \circ } = {140^ \circ }\].
In a triangle sum of all the angles can be represented in the form of degree as well as in the form of radians.

In a triangle, Sum of all angles \[ = {180^ \circ } = {\pi ^c}\], where \[{\pi ^c}\] is called \[\pi \] radian.

Complete step-by-step solution:
So, if any angle is given as a degree form then we will try to convert it into radian first, and then will try to find its supplementary angle.
Let's say, one angle is given as \[{60^ \circ }\].
So, if we convert \[{60^ \circ }\] into its radian, then we will perform the following steps:
\[{180^ \circ } = {\pi ^c}\]
Or, \[{1^ \circ } = {\left( {\dfrac{\pi }{{180}}} \right)^c}\]
So, \[{60^ \circ } = {\left( {60 \times \dfrac{\pi }{{180}}} \right)^c}\]
Or, \[{60^ \circ } = {\left( {\dfrac{\pi }{3}} \right)^c}\].
Now, to find the Supplementary of \[{60^ \circ }\] in radian, we will have to simply subtract it from\[{\pi ^c}\].
So, supplementary of \[{60^ \circ }\] in radian will be \[\left( {\pi - \dfrac{\pi }{3}} \right) = \dfrac{{3\pi - \pi }}{3} = \dfrac{{2\pi }}{3}\] radian.
So, the general rule to find any supplementary angle of any angle is:
If it is given in degree form, then we have to convert it into its radian first and then we will subtract it from \[\pi \] radian.
Or, if it is given radian itself, then we will simply subtract it from \[\pi \] radian.

So, Supplementary of two angles means that:
 \[\angle 1 + \angle 2 = {180^ \circ } = {\pi ^c}\].

Note: On the other hand complementary of two angles means that the sum of these two angles is equal to \[{90^ \circ }\] or \[\dfrac{\pi }{2}\] radian.
In that case we have to subtract the given angle’s radian value from \[\dfrac{\pi }{2}\] to get the complementary angle in radian form.