Question

How do you find the region inside cardioid $ r = 1 + \cos \theta $ and outside the circle $ r = 3\cos \theta $ ?

Answer 1

Hint: In this question, we are given the equation of two curves and we have to find their common area based on the given condition. For that, we first need to graph the given functions and then shade the required area from the given information. We will find the area of the shaded region by using integration over limits.

Complete step-by-step answer:
To find the region inside cardioid $ r = 1 + \cos \theta $ and outside the circle $ r = 3\cos \theta $ , we will first draw both of them on the same plane and then find their point of intersection. Then using the given information, we will shade the region whose area we have to find.
The point of intersection of $ r = 1 + \cos \theta $ and $ r = 3\cos \theta $ is
 $
  1 + \cos \theta = 3\cos \theta \\
  1 = 2\cos \theta \\
   \Rightarrow \cos \theta = \dfrac{1}{2} \\
   \Rightarrow \theta = {\cos ^{ - 1}}(\dfrac{1}{2}) \\
   \Rightarrow \theta = \pm \dfrac{\pi }{3} \;
  $
So, two curves intersect at $ \theta = \pm \dfrac{\pi }{3} $

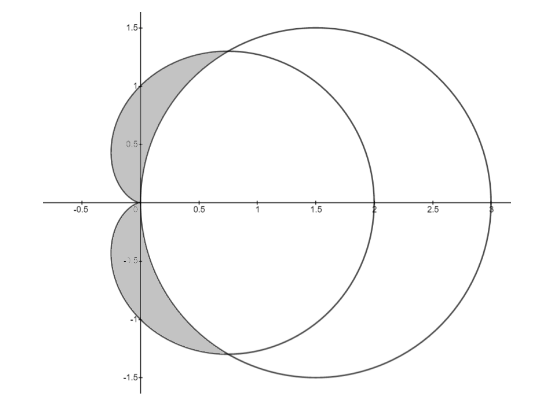
Area of the cardioid,
\[
  {A_1} = \int\limits_{\dfrac{\pi }{3}}^\pi {\dfrac{1}{2}{{(1 + \cos \theta )}^2}d\theta } = \dfrac{1}{2}\int\limits_{\dfrac{\pi }{3}}^\pi {(1 + {{\cos }^2}\theta + 2\cos \theta )d\theta } = \dfrac{1}{2}\int\limits_{\dfrac{\pi }{3}}^\pi {(1 + \dfrac{{\cos 2\theta + 1}}{2} + 2\cos \theta )d\theta } \\
   \Rightarrow {A_1} = \dfrac{1}{2}[\theta + \dfrac{1}{2}(\dfrac{{\sin 2\theta }}{2} + \theta ) + 2\sin \theta ]_{\dfrac{\pi }{3}}^\pi \\
   \Rightarrow {A_1} = \dfrac{1}{2}[\dfrac{{3\theta }}{2} + \dfrac{{\sin 2\theta }}{4} + 2\sin \theta ]_{\dfrac{\pi }{3}}^\pi \\
   \Rightarrow {A_1} = \dfrac{1}{2}[\dfrac{{3\pi }}{2} + 0 + 0 - \dfrac{\pi }{2} - \dfrac{{\sqrt 3 }}{8} - \sqrt 3 ] \\
   \Rightarrow {A_1} = \dfrac{1}{2}[\pi + \dfrac{{ - 9\sqrt 3 }}{8}] \\
   \Rightarrow {A_1} = \dfrac{\pi }{2} - \dfrac{{9\sqrt 3 }}{{16}} \;
 \]
Area of the circle –
 $
  {A_2} = \int\limits_{\dfrac{\pi }{3}}^{\dfrac{\pi }{2}} {\dfrac{1}{2}{{(3\cos \theta )}^2}d\theta } \\
   \Rightarrow {A_2} = \dfrac{9}{2}\int\limits_{\dfrac{\pi }{3}}^{\dfrac{\pi }{2}} {\dfrac{{\cos 2\theta + 1}}{2}d\theta } \\
   \Rightarrow {A_2} = \dfrac{9}{4}[\dfrac{{\sin 2\theta }}{2} + \theta ]_{\dfrac{\pi }{3}}^{\dfrac{\pi }{2}} \\
   \Rightarrow {A_2} = \dfrac{9}{4}[0 + \dfrac{\pi }{2} - \dfrac{{\sqrt 3 }}{4} - \dfrac{\pi }{3}] \\
   \Rightarrow {A_2} = \dfrac{9}{4}[\dfrac{\pi }{6} - \dfrac{{\sqrt 3 }}{4}] \\
   \Rightarrow {A_2} = \dfrac{{3\pi }}{8} - \dfrac{{9\sqrt 3 }}{{16}} \;
  $
Area of the shaded region,
 $
  A = {A_1} - {A_2} \\
   \Rightarrow A = \dfrac{\pi }{2} - \dfrac{{9\sqrt 3 }}{{16}} - (\dfrac{{3\pi }}{8} - \dfrac{{9\sqrt 3 }}{{16}}) \\
   \Rightarrow A = \dfrac{\pi }{2} - \dfrac{{9\sqrt 3 }}{{16}} - \dfrac{{3\pi }}{8} + \dfrac{{9\sqrt 3 }}{{16}} \\
   \Rightarrow A = \dfrac{\pi }{8} \;
  $
This is the area of the shaded region in the first and the second quadrant. We see that by symmetry, the area of the shaded region in the first and the second quadrant is equal to the area of the shaded region in the third and the fourth quadrant.
So, the total area is $ 2 \times \dfrac{\pi }{8} = \dfrac{\pi }{4} $
Hence the region inside cardioid $ r = 1 + \cos \theta $ and outside the circle $ r = 3\cos \theta $ is equal to $ \dfrac{\pi }{4} $ .
So, the correct answer is “ $ \dfrac{\pi }{4} $ ”.

Note: We integrate the area of the cardioid and the circle from $ \dfrac{\pi }{3} $ to $ \pi $ and $ \dfrac{\pi }{3} $ to $ \dfrac{\pi }{2} $ respectively because we need to find the area under that region only. But one may get confused that we have taken the upper limit of cardioid as $ \pi $ and that of the circle as $ \dfrac{\pi }{2} $ . We see that their point of intersection is zero and $ \pm \dfrac{\pi }{3} $ , and $ 1 + \cos \theta $ is zero at $ \theta = \pi $ while $ 3\cos \theta $ is zero at $ \theta = \dfrac{\pi }{2} $ .