Question

Find the principal value of ${\cot ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right)$

Answer 1

Hint: The principal value of an inverse trigonometric function at a point x is the value of the inverse function at the point x, which lies in the range of the principal branch.The principal value of the cotangent function is from $\left( {0,\pi } \right)$. From the table we will find the value of the function within the principal range, and use the property that-
$cot^{-1}(-x) = 180^o - cot^{-1}(x)$

Complete step-by-step answer:
The values of the cotangent functions are-

Function	$0^o$	$30^o$	$45^o$	$60^o$	$90^o$
cot	Not defined		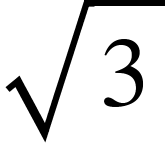1		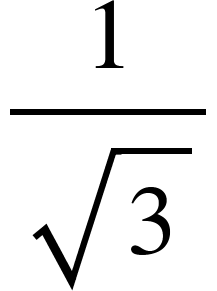0

In the given question we need to find the principal value of ${\cot ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right)$. We know for the cotangent function to be negative, the angle should be obtuse, that is greater than $90^o$. We know that $\cot {60^{\text{o}}} = \dfrac{1}{{\sqrt 3 }}$. This means that the value of ${\cot ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) = {60^{\text{o}}}$. So the value of the given expression can be calculated as-
${\cot ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = {180^{\text{o}}} - {60^{\text{o}}} = {120^{\text{o}}}$
${\cot ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = \dfrac{{2{{\pi }}}}{3}$
This is the required value.

Note: In such types of questions, we need to strictly follow the range of the principal values that have been specified. The principal value of cotangent in the question should always be between $0^o$ and $180^o$. This is because there can be infinite values of any inverse trigonometric functions.One common mistake is that students use the wrong range of principal values for both the tangent and the cotangent function, we should remember the ranges for both the functions.