Question

Find the number of points of non-differentiability of \[f\left( x \right)=\max \{\sin x,\cos x,0\}\] in $x\in \left( 0,2\pi \right)$

Answer 1

Hint: To solve this question we will draw graph of sin x and cos x. Then we will combine the graph and delete the minimum part so that we get the graph of \[f\left( x \right)=\max \{\sin x,\cos x,0\}\] .
Now we will check the points where the function is non-differentiable as at that point the curve will not be smooth.

Complete step-by-step solution:
Now let us first understand the concept of differentiability.
A function is called differentiable at a point if its derivative exists at a point.
Now a function is called differentiable if it is differentiable at each point in its domain.
Now let us see the condition for which the function is differentiable.
A function f is said to be differentiable at point c if $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( c+h \right)-f\left( c \right)}{h}$ exists.
Now to check if the limits exist we will check if the left-hand limit is equal to the right-hand limit.
Now let us understand this geometrically.
Now geometrically we know that derivative at a point is nothing but the slope of the curve at that point.
For this derivative to exist we need the curve to be smooth at that point.
Hence if a curve is smooth at a point then we can say it is differentiable
If a curve has sharp point on the curve then the point will be non-differentiable.
Now for example consider $\left| x \right|$ .
We know that the graph of $\left| x \right|$ is

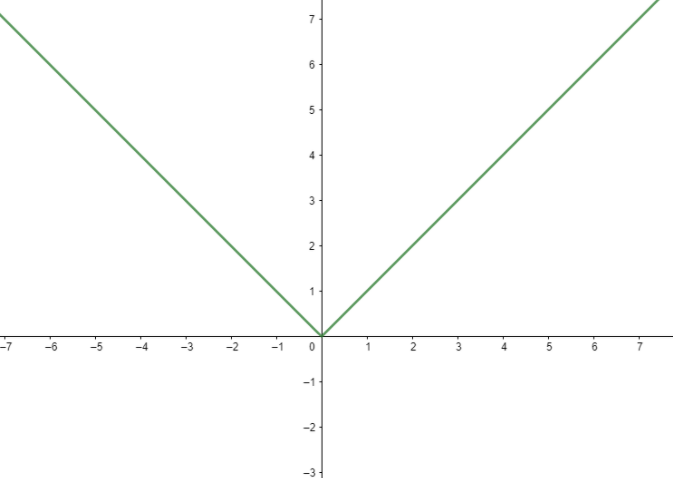
Now we can see from the graph that the graph has a sharp point at $x = 0. $
Hence by looking at the graph we can say that the function is not differentiable at $x = 0.$
Now consider the given function \[f\left( x \right)=\max \{\sin x,\cos x,0\}\] in $x\in \left( 0,2\pi \right)$
Now let us first check the graph of sin x for $x\in \left( 0,2\pi \right)$ .

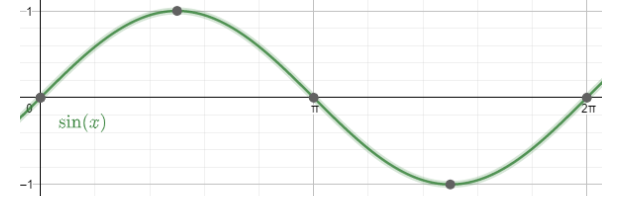
Now let us also check the graph of cos x for $x\in \left( 0,2\pi \right)$ .

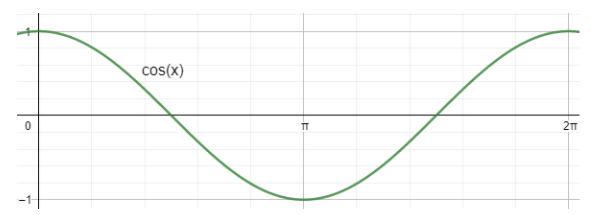
Now we will merge the graph and just consider the maximum part. That means if $\cos x > \sin x$ then we will consider cos x. Similarly, if $\sin x \text{ is } > \cos x$, then we will consider sin x. Now if we have both negative then we will take 0. Hence we will get the graph for \[f\left( x \right)=\max \{\sin x,\cos x,0\}\]

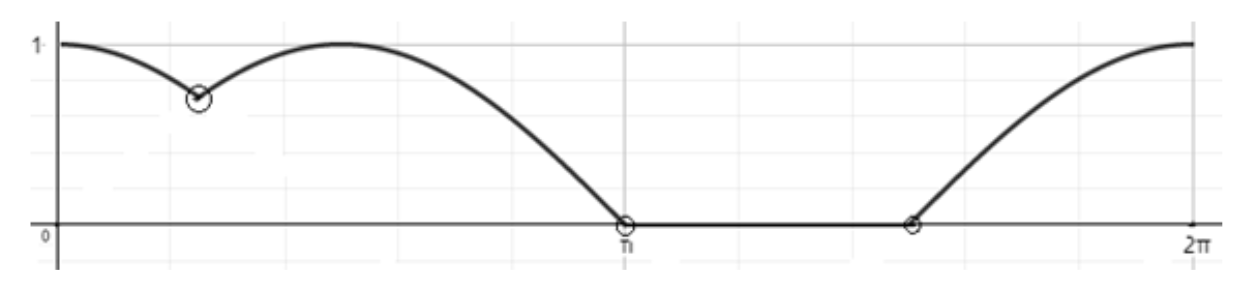
Hence as we can see that the function is sharp at three points and hence is non-differentiable at three points.

Note: Note that whenever the function is defined as a maximum or minimum of two or more functions, we use a geometrical approach to the question as we can easily draw graphs for such functions. Also here we can ask that the function is also not differentiable at point x = 0 and x = $2\pi $ but we have not counted these points as they are not in our domain. The domain of given function is $x\in \left( 0,2\pi \right)$ . Hence if the domain would have been $x\in \left[ 0,2\pi \right]$ then we would get 5 non-differentiable points.