
Find the number of divisors of 8064.
Answer
614.1k+ views
Hint: Apply prime factorisation to find the prime factors of the given number and then apply formula to find the number of divisors of the given number.
The given number is 8064.
First we find all the prime factors of the given number.
Prime factors are numbers which are divisible by itself, that is, it has ‘one’ and itself as the factors.
Now let’s find all the prime factors of 8064 using prime factorisation method
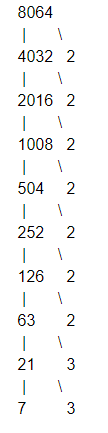
So, 8064 can be written as,
$8064=2\times 2\times 2\times 2\times 2\times 2\times 2\times 3\times 3\times 7$
By grouping, we get
$8064={{2}^{7}}\times {{3}^{7}}\times {{7}^{1}}.........\left( 1 \right)$
Now to find the number of divisors we will use the formula,
$d\left( n \right)=\left( p+1 \right)\times \left( q+1 \right)\times \left( r+1 \right)$
Where ‘n’ is the number and ‘p, q, r’ are the powers of prime factors of the numbers or they are the exponents of prime factorisation.
Such that a number can be represented as,
$n={{a}^{p}}\times {{b}^{q}}\times {{c}^{r}}.........\left( 2 \right)$
Where ‘a, b, c’ are prime factors of ‘n’
Now applying this formula in our problem, we get
Comparing equation (1) and (2), we get
P=7, q=2, r=1
So the number of divisors will be
$d\left( 8064 \right)=\left( 7+1 \right)\times \left( 2+1 \right)\times \left( 1+1 \right)$
Solving we get
$\begin{align}
& d\left( 8064 \right)=8\times 3\times 2 \\
& \Rightarrow d\left( 8064 \right)=48 \\
\end{align}$
So the number of divisors of 8064 is 48.
Note: Student forgets to add one in the divisor formula i.e.,
$d\left( n \right)=\left( p+1 \right)\times \left( q+1 \right)\times \left( r+1 \right)........\left( A \right)$
Will be mistakenly written as,
$d\left( n \right)=p\times q\times $$r........\left( B \right)$
The answer we get in both cases does not match and the student will end up in the wrong answer if he uses formula (B) instead of (A).
The given number is 8064.
First we find all the prime factors of the given number.
Prime factors are numbers which are divisible by itself, that is, it has ‘one’ and itself as the factors.
Now let’s find all the prime factors of 8064 using prime factorisation method
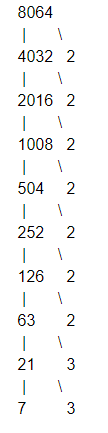
So, 8064 can be written as,
$8064=2\times 2\times 2\times 2\times 2\times 2\times 2\times 3\times 3\times 7$
By grouping, we get
$8064={{2}^{7}}\times {{3}^{7}}\times {{7}^{1}}.........\left( 1 \right)$
Now to find the number of divisors we will use the formula,
$d\left( n \right)=\left( p+1 \right)\times \left( q+1 \right)\times \left( r+1 \right)$
Where ‘n’ is the number and ‘p, q, r’ are the powers of prime factors of the numbers or they are the exponents of prime factorisation.
Such that a number can be represented as,
$n={{a}^{p}}\times {{b}^{q}}\times {{c}^{r}}.........\left( 2 \right)$
Where ‘a, b, c’ are prime factors of ‘n’
Now applying this formula in our problem, we get
Comparing equation (1) and (2), we get
P=7, q=2, r=1
So the number of divisors will be
$d\left( 8064 \right)=\left( 7+1 \right)\times \left( 2+1 \right)\times \left( 1+1 \right)$
Solving we get
$\begin{align}
& d\left( 8064 \right)=8\times 3\times 2 \\
& \Rightarrow d\left( 8064 \right)=48 \\
\end{align}$
So the number of divisors of 8064 is 48.
Note: Student forgets to add one in the divisor formula i.e.,
$d\left( n \right)=\left( p+1 \right)\times \left( q+1 \right)\times \left( r+1 \right)........\left( A \right)$
Will be mistakenly written as,
$d\left( n \right)=p\times q\times $$r........\left( B \right)$
The answer we get in both cases does not match and the student will end up in the wrong answer if he uses formula (B) instead of (A).
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE

Discuss the various forms of bacteria class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

An example of chemosynthetic bacteria is A E coli B class 11 biology CBSE




