Question

Find the midpoint of each diagonal of the quadrilateral with vertices $P(1,3)$, $Q(6,5)$, $R(8,0)$ and $S(3, - 2)$?

Answer 1

Hint: In the given question, we are required to find the midpoints of diagonals of a quadrilateral whose coordinates of vertices are given to us. The required task can be done using the midpoint formula where we find the midpoint of a line segment using a predefined formula. We just plug in the values of coordinates of vertices given to us to find out the midpoints of the diagonals.

Complete step by step solution:
Every quadrilateral has two diagonals. The quadrilateral PQRS has two diagonals PR and QS. The midpoints of these two diagonals can be calculated using the midpoint formula.

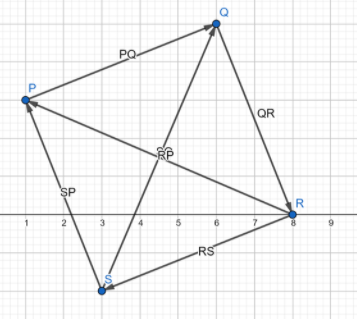
For the diagonal PR, coordinates of endpoint P are $(1,3)$ and that of R are $(8,0)$.
Using midpoint formula, Midpoint$ = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
So, Midpoint of diagonal PR is\[\left( {\dfrac{{1 + 8}}{2},\dfrac{{3 + 0}}{2}} \right) = \left( {\dfrac{9}{2},\dfrac{3}{2}} \right)\]
So, the midpoint of diagonal PR is \[\left( {\dfrac{9}{2},\dfrac{3}{2}} \right)\]
Similarly using midpoint formula,
We get the midpoint of diagonal QS as $\left( {\dfrac{{6 + 3}}{2},\dfrac{{5 + ( - 2)}}{2}} \right)$.
So, Midpoint of the diagonal QS is \[\left( {\dfrac{9}{2},\dfrac{3}{2}} \right)\].
Hence the midpoints of the diagonals of the quadrilateral PQRS whose coordinates of vertices are given to us are \[\left( {\dfrac{9}{2},\dfrac{3}{2}} \right)\] and \[\left( {\dfrac{9}{2},\dfrac{3}{2}} \right)\], So we conclude that the midpoint of both the diagonals is same as \[\left( {\dfrac{9}{2},\dfrac{3}{2}} \right)\]. Hence, the given quadrilateral is a parallelogram that has diagonals of a parallelogram bisecting each other.

Note:
We must remember the properties of each quadrilateral. The diagonals of a parallelogram bisect each other. Hence, the quadrilateral given to us in the question is a parallelogram and this can also be verified by calculating the sides of the quadrilateral and observing that the length of opposite sides are equal as well.