Question

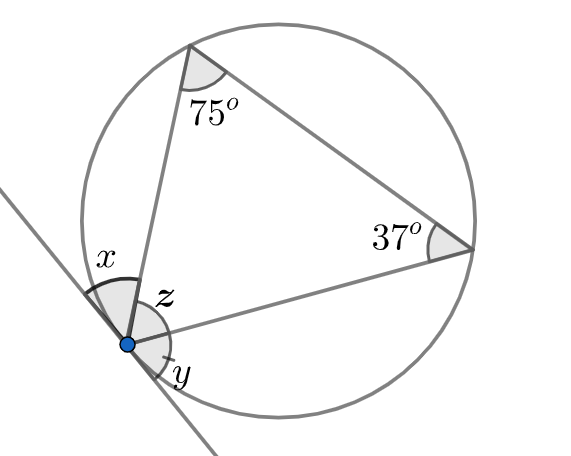
Find the measure of angles $z$ . (in degrees)

$(A)75$
$(B)68$
$(C)37$
$(D)$ None of these

Answer 1

Hint: Problems of this type are actually the simplest ones if the unnecessary data are ignored. There is an inscribed triangle into a circle along with a straight line as its tangent but to solve for the measure of $z$ the angles $x$ and $y$ becomes unnecessary. Hence, we will just simply apply the property of triangles, which is the summation of all the interior angles of a triangle to be ${{180}^{\circ }}$ .

Complete step-by-step answer:
In the problem we have a triangle inscribed in a circle. Also, a straight line is present as the tangent of the circle where the vertex of the triangle meets the circle.
But to find the measure of the interior angle $z$of the triangle we just require the other two interior angles of the triangle. Therefore, both the concept of the circle inscribing a triangle and the straight line being a tangent are just unnecessary data which is of no use.
Hence, we don’t require any of the angles $x$ and $y$
We know that the summation of the three interior angles is ${{180}^{\circ }}$.
So, if any of the two angles are already known we can subtract the summation of the two known angles from $180$ to get the measure of the unknown angle.
Hence, $z+75+37=180$
$\Rightarrow z=180-75-37$
Further, simplifying we get
$\Rightarrow z=68$
Therefore, we conclude that the measure of angle $z$ is ${{68}^{\circ }}$ (B).
So, the correct answer is “Option B”.

Note: While finding the measure of the angle $z$we must not get emphasized by the circle that is inscribing the triangle and also the straight line that is present as the tangent of the circle as the angles $x$ and $y$as they are of no use. Also, while solving for $z$ we must check whether the known angles of the triangle are interior angles or exterior angles. Otherwise, the exterior angles must be converted to the interior ones to get the exact result.