Question

Find the locus of the third vertex of a right-angled triangle, the ends of whose hypotenuse are (4, 0), (0, 4).

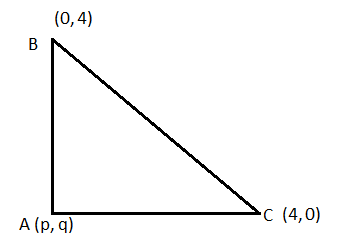
Answer 1

Hint: A locus is a set of all points whose location satisfies or is determined by one or more specified conditions. In other words, the set of points that satisfy some property is often called the locus of points satisfying this property.
The locus of a point P is such that it is equidistant from two given points. A and b that is, $PA = PB$. The locus of the point at fixed distance d, from point P, is a circle with given point P as its center and d as its radius. Here in this question, we can use the distance formula for two given points.
Distance formula $ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $.

Complete step by step solution:
Let the point be (p, q).
Then, $\vartriangle ABC$ is right-angled at point A.
$ \Rightarrow B{C^2} = A{B^2} + A{C^2}$ (By Pythagoras theorem)
$\eqalign{
  & \Rightarrow {\left( {4 - 0} \right)^2} + {\left( {0 - 4} \right)^2} = {\left( {p - 0} \right)^2} + {\left( {q - 4} \right)^2} + {\left( {p - 4} \right)^2} + {\left( {q - 0} \right)^2} \cr
  & \Rightarrow 16 + 16 = {p^2} + {q^2} + 16 - 8q + {p^2} + 16 - 8p + {q^2} \cr
  & \Rightarrow 32 = 2\left( {{p^2} + {q^2} - 4p - 4q} \right) + 32 \cr} $
Or, ${p^2} + {q^2} - 4p - 4q = 0$.
Replacing $p \to x$ and $q \to y$.

$\therefore {x^2} + {y^2} - 4p - 4q = 0$ is the locus of the equation.

Note: We can also find this finding slope of two lines AB as ${m_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$, and AC as ${m_2} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$.
And for perpendicular lines ${m_1}{m_2} = - 1$.
We get the required locus of the third vertex.