Question

A gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends length 5 cm and diameter 2.8 cm.

Answer 1

Hint: We will first find the radius by taking half the diameter. Then, find the height of the cylinder of gulab jamun by subtracting the radius of both the hemispheres from the total height of the gulab jamun. Then, find the volume of the gulab jamun by adding the volume of cylinder and volume of two hemispheres. The volume of the cylinder is $\pi {r^2}h$, where $r$ is the radius of the cylinder and $h$ is the height of the cylinder and the volume of the hemisphere is $\dfrac{2}{3}\pi {r^3}$. Then, take 30% of the volume calculated to find the volume of the syrup.

Complete step-by-step answer:
Each gulab jamun is of the shape of a cylinder.
The radius is half the diameter.
The diameter is 2.8 cm. Then, radius is $\dfrac{{2.8}}{2} = 1.4cm$

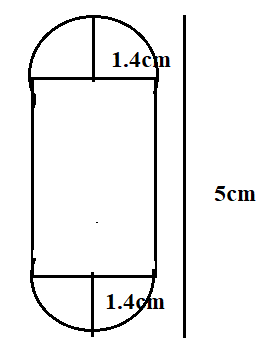
Then, we will calculate the height of the cylinder by subtracting the diameter of the hemisphere from the height of the gulab jamun.
The height of the cylinder is $5 - \left( {1.4 + 1.4} \right) = 5 - 2.8 = 2.2cm$
Hence, the height of the cylinder is 2.2 cm.
The volume of the gulab jamun is the sum of the volume of cylinder and volume of two hemisphere.
We know that the volume of the cylinder is $\pi {r^2}h$, where $r$ is the radius of the cylinder and $h$ is the height of the cylinder.
And the volume of the hemisphere is $\dfrac{2}{3}\pi {r^3}$.
Hence, the volume of the gulab jamun is $\pi {r^2}h + 2\left( {\dfrac{2}{3}\pi {r^3}} \right)$
On substituting the value of $r$, $h$ and $\pi = \dfrac{{22}}{7}$, we will get,
$\dfrac{{22}}{7}{\left( {1.4} \right)^2}\left( {2.2} \right) + 2\left( {\dfrac{2}{3}\left( {\dfrac{{22}}{7}} \right){{\left( {2.2} \right)}^3}} \right) = 25.05c{m^3}$
There are 45 gulab jamuns, so to find the total volume of the gulab jamun we will multiply the volume of 1 gulab jamun by 45.
$25.05\left( {45} \right) = 1127.25$
Now, we are given that the sugar syrup is 30% of the volume of the cylinder.
Then, volume of the sugar syrup used is $\dfrac{{30}}{{100}}\left( {1127.25} \right) = 338.175c{m^3}$
Therefore, sugar syrup found in gulab jamun is approximately $338c{m^3}$.
Note: Volume of two hemispheres is equal to one sphere. Therefore, we can find the volume of the gulab jamun by adding the volume of the cylinder and the volume of the sphere. Students must remember the formula in order to avoid mistakes. Also, the volume of any object is measured in cubic units.