Question

Find the length of an arc of semicircle?

Answer 1

Hint: Find the arc length by applying the formula to the supplied radius of \[r=10\] cm. Arc length \[=\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r\], where r is the radius and \[\theta \] is the central angle.

Complete step-by-step solution:
The diameter of a circle is defined as the diameter of a circle measured from the center to another point on the circle in the query.
The radius of a circle is the distance between the center and the perimeter of a circle.
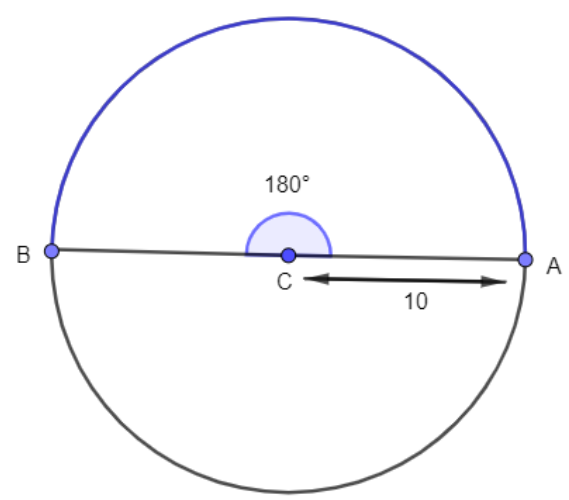
As a result, the radius of the circle in the question is \[r=10\] cm.
The arc of a circle is a section of the circle's circumference.
Here, we must determine the length of the arc that forms \[{{180}^{\circ }}\] angle with the center.
That is, if the two arc end points are added together with the center, the resulting angle is \[{{180}^{\circ }}\].
We already know that the arc length, radius, and angle all have a relationship.
Arc length \[=\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r\]
Here, r is the radius of the circle which is 10 cm here.
Angle\[\theta \] is the corresponding angle, which is \[{{180}^{\circ }}\] here.
Therefore, the arc length is
\[=\dfrac{{{180}^{\circ }}}{{{360}^{\circ }}}\times 2\pi \times 10=\dfrac{1}{2}\times 20\pi =10\pi \]
Hence the arc length is \[10\pi \] cm or we can put the value of \[\pi =\dfrac{22}{7}\]
The arc length is \[=10\times \dfrac{22}{7}=\dfrac{220}{7}\,\,\text{cm}\].

Note: Alternatively we can say that, since the corresponding central angle of the arc is \[{{180}^{\circ }}\], which half of is \[{{360}^{\circ }}\], the arc is essentially a semicircle without the diameter. An arc is the part of a circle which is formed due to a particular angle.