Question

Find the lateral surface area of one cuboid whose dimensions are l = 22cm, b = 12cm, h = 7.5cm.
(a) 511 $c{{m}^{2}}$
(b) 510 $c{{m}^{2}}$
(c) 512 $c{{m}^{2}}$
(d) 513 $c{{m}^{2}}$

Answer 1

Hint: We will use the formula given by $2\left( l+b \right)\times h$ which is known as the lateral surface area of the cuboid. With the help of this formula we will be able to solve the question. Here l is the length of the cuboid, b is the breadth and h is the height of the cuboid.

Complete step-by-step answer:
To solve the question we will first consider the term lateral surface. Lateral surface is actually counted on the curved surface and the area of the top. So, we will find the lateral surface area of a cuboid by considering the surface of the cuboid and its area of the top. The area of the top of the cuboid is basically the area of the square which is given by the side square.
But if we need to find the lateral surface area of a cuboid then along with the area of the square on the top of the cuboid we will also take the surface of the cuboid. This can be numerically written as $2\left( l+b \right)\times h$. The diagram according to the given dimensions in the question is given below.

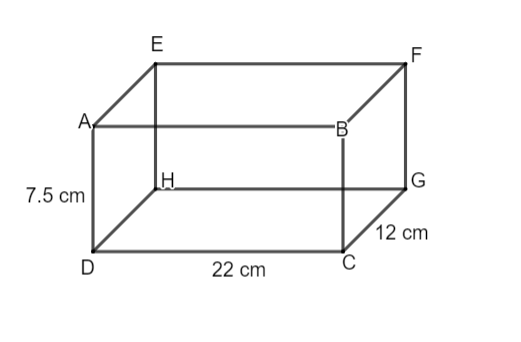
As we are given the length of the cuboid as 22 cm which is denoted by l, breadth of the cuboid as 12 cm which is denoted by b and the height of the cuboid as 7.5 cm which is denoted by h so, the formula of the cuboid gets converted into a new equation by the substitution of these values. Thus, we get
$\begin{align}
  & \text{area of cuboid = }2\left( l+b \right)\times h \\
 & \Rightarrow \text{area of cuboid = 2}\left( 22cm+12cm \right)\times 7.5cm \\
 & \Rightarrow \text{area of cuboid = 2}\left( 34cm \right)\times 7.5cm \\
 & \Rightarrow \text{area of cuboid = }68cm\times 7.5cm \\
 & \Rightarrow \text{area of cuboid = }510c{{m}^{2}} \\
\end{align}$
Hence, the area of the cuboid is 510 centimetres square.

Note: In case we have to find the total surface area, then we will use the formula of the total surface area of the cuboid as $2\left( lh+bh+hl \right)$. Before solving the question one should notice the units of the dimensions of the cuboid. This is because if the units are not the same, then we will eventually get the wrong answer. Always solve the question by converting into a single unit only. We must not forget to mention the units in the answer as well correctly.