Question

How do you find the inverse of $f\left( x \right)={{x}^{2}}-2$ from $x\le 0$ and graph both $f$ and ${{f}^{-1}}$?

Answer 1

Hint: We first explain the expression of the function as we take $y=f\left( x \right)={{x}^{2}}-2$. We convert the function from $y$ of $x$ to $x$ of $y$. The inverse function on being conjugated gives the value of $x$. At the end we interchange the terms to make it a general equation.

Complete step-by-step solution:
We need to find the inverse of the equation of ${{x}^{2}}-2$.
The given equation is a function of $x$ where we can write $y=f\left( x \right)={{x}^{2}}-2$.
If we take the inverse of the equation, we will get $x={{f}^{-1}}\left( y \right)$.
The given function was of $x$. We convert it to a function of $y$ and that becomes the inverse of $y={{x}^{2}}-2$.
We need to express the value of $x$ with respect to $y$.
We first add 2 on both sides of the equation and get
\[\begin{align}
  & y={{x}^{2}}-2 \\
 & \Rightarrow y+2={{x}^{2}} \\
\end{align}\]
Now we take square root on both sides and get
\[\begin{align}
  & {{x}^{2}}=y+2 \\
 & \Rightarrow x=\pm \sqrt{y+2} \\
\end{align}\]
Therefore, the expression of $x$ with respect to $y$ is \[x=\pm \sqrt{y+2}\].
Now as we know any general expression of any function is defined by the function of $x$.
We try to interchange the position of $x$ and $y$ in the equation \[x=\pm \sqrt{y+2}\] to form the inverse equation in general form.
From \[x=\pm \sqrt{y+2}\], we get \[y=\pm \sqrt{x+2}\]. So, $y={{f}^{-1}}\left( x \right)=\pm \sqrt{x+2}$
Therefore, the inverse function of $f\left( x \right)={{x}^{2}}-2$ is \[y=\pm \sqrt{x+2}\].
The range of the function $f\left( x \right)={{x}^{2}}-2$ is equal to the domain for the ${{f}^{-1}}\left( x \right)=\pm \sqrt{x+2}$ and it is $\left[ -2,\infty \right)$.
The graphs for $f\left( x \right)={{x}^{2}}-2$ is

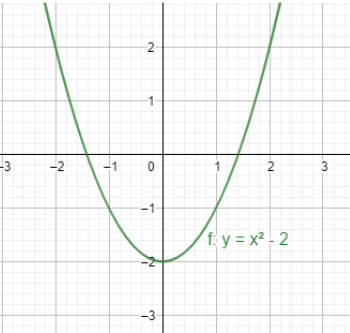
The graphs for ${{f}^{-1}}\left( x \right)=\pm \sqrt{x+2}$ is

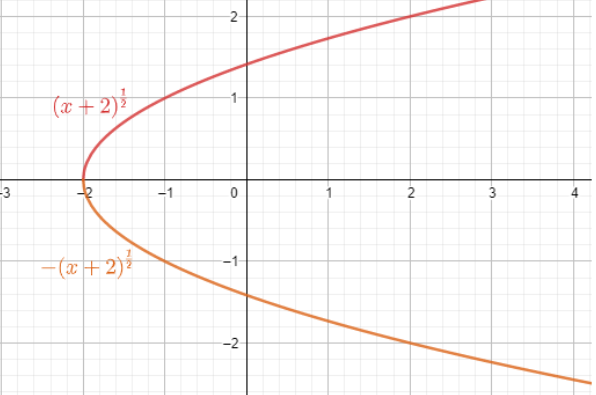
Note: All quadratic equations cannot have an inverse. It’s necessary to understand the concept of domain as the inverse function has to be well-defined. For our inverse function of ${{f}^{-1}}\left( x \right)=\pm \sqrt{x+2}$, the restriction is $x\ge -2$. Otherwise, the function becomes imaginary.