Question

Find the exact value of ${\csc ^{ - 1}}( - 1)$

Answer 1

Hint: Here in the question we are supposed to find the inverse trigonometric function to find the angle. This means the value in the bracket of trigonometric functions given here is an exact value of the function at a certain angle. So we have to find that angle in this question. For that we will see the range for Cosecant and then check for the principal values of trigonometric functions.

Complete step by step solution:
Let us suppose that $y = {\csc ^{ - 1}}( - 1)$ ----equation (1)
As we can see we have converted this into an equation by putting two expressions on both sides of the sign ‘equals to’ (=).
We can compare equation (1) with this equation: $y = \;f(x)$ -----equation (2)
From equation (1) & (2) we have: \[f(x) = {\csc ^{ - 1}}( - 1)\]
This means we can operate on equation (1) and shift the inverse trigonometric function on the LHS.
$ \Rightarrow \csc y = - 1$----equation (3)
We know that
\[\csc {90^ \circ } = 1\]
Since $\csc y$ is negative in equation (3) so we have to recall the signs of trigonometric functions in all the quadrants which is given in figure given below

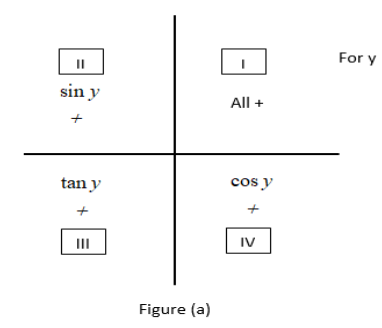
From figure (a) we can certainly say that $\sin y$ is positive in 1 st & 2 nd quadrant and similarly $\csc y$ will be positive in the same because both are reciprocal ratios of a triangle i.e. $\sin y = \dfrac{1}{{\csc y}}$ which means it has to be negative in 3 rd and 4 th quadrants.

So the value of $\csc y$ in 3 rd quadrant:
${180^ \circ } + {90^ \circ } = \;{270^ \circ }$
Similarly, the value of $\cot y$ in 4 th quadrant:
${360^\circ } - {90^ \circ } = {270^ \circ }$
From this we can find the value of the equation (3)
\[
\Rightarrow \csc y = - \;1 \\
\Rightarrow \;y = \;{270^ \circ } \\
\]
To convert these degree values into radian values we have to multiply it by $\dfrac{\pi }{{180}}$i.e.
$
y = 270^\circ \\
y = 270 \times \dfrac{\pi }{{180}} \\
y = \dfrac{{3\pi }}{2} \\
$
But we have to find the exact value of the given inverse function for that we check for the range of inverse function cotangent i.e.
$
{\csc ^{ - 1}}(b) = \theta \;;\;where\;\theta \in \;[ - \dfrac{\pi }{2},\dfrac{\pi }{2}] - \{ 0\} $
From this we can say that
$
{\csc ^{ - 1}}( - 1) = \dfrac{{3\pi }}{2} = - \dfrac{\pi }{2}{\text{ because}} - \dfrac{\pi }{2} \in [ -
\dfrac{\pi }{2},\dfrac{\pi }{2}] - \{ 0\} \\
\Rightarrow y = - \dfrac{\pi }{2}\; \\
$

Note: We can find angles of trigonometric functions in the manner given above but the important part is to check the range of these inverse trigonometric functions in order to find the exact solution. Changing degree values of angles into radians is not necessary but angles in radians are more preferable at this level.