Question

How do you find the exact value of $arc\cos \left( -\dfrac{1}{\sqrt{2}} \right)$?

Answer 1

Hint: We explain the function $\arccos \left( x \right)$. We express the inverse function of cos in the form of $\arccos \left( x \right)={{\cos }^{-1}}x$. We draw the graph of $\arccos \left( x \right)$ and the line $x=-\dfrac{1}{\sqrt{2}}$ to find the intersection point as the solution.

Complete step by step answer:
The given expression is the inverse function of trigonometric ratio cos.
The arcus function represents the angle which on ratio cos gives the value.
So, $\arccos \left( x \right)={{\cos }^{-1}}x$. If \[\arccos \left( x \right)={{\cos }^{-1}}x=\alpha \] then we can say $\cos \alpha =x$.
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of $2\pi $.
The general solution for that value where $\cos \alpha =x$ will be $2n\pi \pm \alpha ,n\in \mathbb{Z}$.
But for $\arccos \left( x \right)$, we won’t find the general solution. We use the principal value. For ratio tan we have $0\le \arccos \left( x \right)\le \pi $.
The graph of the function is

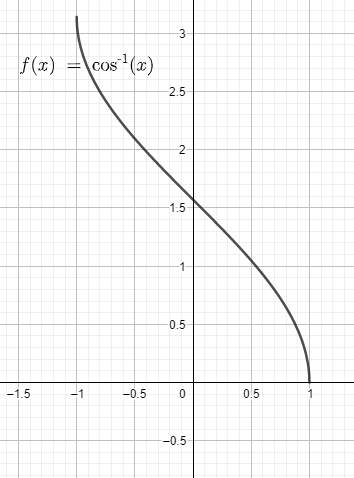
\[\arccos \left( x \right)={{\cos }^{-1}}x=\alpha \] gives the angle $\alpha $ behind the ratio.
We now place the value of $x=-\dfrac{1}{\sqrt{2}}$ in the function of \[\arccos \left( x \right)\].
Let the angle be $\theta $ for which $arc\cos \left( -\dfrac{1}{\sqrt{2}} \right)=\theta $. This gives $\cos \theta =-\dfrac{1}{\sqrt{2}}$.
We know that $\cos \theta =-\dfrac{1}{\sqrt{2}}=\cos \left( \dfrac{\pi }{2}+\dfrac{\pi }{4} \right)$ which gives $\theta =\left( \dfrac{\pi }{2}+\dfrac{\pi }{4} \right)=\dfrac{3\pi }{4}$
For this we take the line of $x=-\dfrac{1}{\sqrt{2}}$ and see the intersection of the line with the graph $\arccos \left( x \right)$.

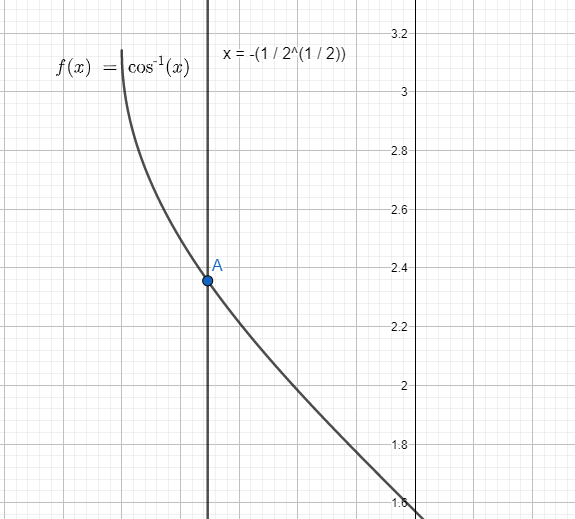
We get the value of y coordinates as $\dfrac{3\pi }{4}$

Note: If we are finding an $\arccos \left( x \right)$ of a positive value, the answer is between $0\le \arccos \left( x \right)\le \dfrac{\pi }{2}$. If we are finding the $\arccos \left( x \right)$ of a negative value, the answer is between $\dfrac{\pi }{2}\le \arccos \left( x \right)\le \pi $.