Question

How do you find the domain and range of a natural log?

Answer 1

Hint: Logarithmic functions are the inverse of exponential functions. Therefore, the input argument to this function (the domain of the function) is equal to the logarithmic base power of a number. For natural log, the base is $e$ ,where $e$ is the Euler’s number. $\left( {e \approx 2.72} \right)$.

Formula used:
$\ln x = y$
$ \Rightarrow {\log _e}x = y$
$ \Rightarrow x = {e^y}$

Complete step-by-step solution:
We have $\ln x = y$ or $x = {e^y}$.
Since $e$ is a positive number, ${e^y}$ should be a positive number as well for any values of $y$.
That is, $x > 0$
Therefore, the domain of the natural log is:
$0 < x < \infty $
Or $x \in \left( {0,\infty } \right)$ .
Now,
$\mathop {\lim }\limits_{x \to 0} \ln x = - \infty $ and $\mathop {\lim }\limits_{x \to \infty } \ln x = \infty $ --------(1)
Given, $y = \ln x$
$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{1}{x} > 0$ for all $x \in \left( {0,\infty } \right)$
Therefore, we can say that the natural log function is a monotonically increasing function. Thus, from equation (1), we can say that the range of the natural log function is:
$ - \infty < y < \infty $
Or $y \in \left( { - \infty ,\infty } \right)$.
Thus, the domain of the natural log function is $\left( {0,\infty } \right)$ while its range is $\left( { - \infty ,\infty } \right)$ .

Additional information:
The graph of natural log function has a vertical asymptote as $x \to 0$ but does not have a horizontal asymptote.

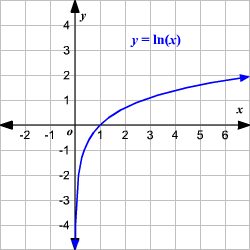
For logarithmic function to any base, as \[x = 0,\ln x = 1\] .
Also, all logarithms have the property of mapping multiplication into addition as:
$\ln xy = \ln x + \ln y$

Note: Natural log functions are found very useful in integration problems involving certain types of integrands. Much of the power of logarithms is their usefulness in solving exponential equations